测试代码见附录
题目
-
在 3 X 3 的空格内,用1,2,…, 9 的9个数字填入9个空格内,使得每行数字组成的十进制数平方根为整数。试用一般图搜索搜索算法求解。
思路:
用队列
open存放1-9中还未使用的数字,对于每个待填的方格,依次尝试open中的数字,利用dfs(从上到下、从左到右)遍历九宫格结果:
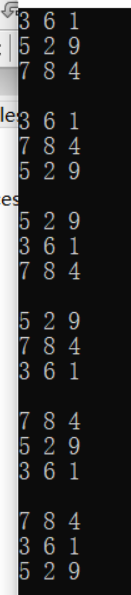
-
分析宽度优先搜索和深度优先搜索的优缺点,举出他们的正例和反例。
宽度优先:
优点:若问题有解,则可找出最优解;对于解决最短或最少问题非常有效
缺点:效率低,组合爆炸问题难以解决
正例:迷宫问题,最短路径问题
反例:旅行商问题
深度优先:
优点:节省大量时间和空间
缺点:不一定能找到解,因为在深度无限搜索树的情况下,最坏的情况可能是不能停机;找到的第一个解不一定是最优解
正例:皇后问题
反例:深度无限的搜索树
-
有一个农夫带一只狐狸、一只小羊和一个菜篮过河。假设农夫每次只能带一样东西过河,考虑安全,无农夫看管时,狐狸和小羊不能在一起,小羊和菜篮不能在一起。试设计求解该问题的状态空间,并画出状态空间图。
用四元组
(a:农夫,b:狐狸,c:小羊,d:菜篮)表示四者的过河情况,其中 1 1 1表示过河, 0 0 0表示未过河,则该问题可被表示为状态(0,0,0,0)到(1,1,1,1)的可选路径,其中(0,1,1,0),(0,1,1,1),(0,0,1,1),(1,0,0,1),(1,0,0,0),(1,1,0,0)为非法状态(不难发现,非法状态是对称状态)- 对于每次状态改变,
a在 0 , 1 0,1 0,1间来回切换,(b,c,d)中每次最多改变一个
根据题意,初步画出状态图

删去非法状态及相关转化方向,化简得到

由非法状态对称性和观察发现,蓝色部分正方体和黑色部分正方体可以组成一个完整的正方体(x010和x101重复),即(除两个重复点外)蓝色点和黑色点成为偶图的两部分,连通二部的通路为合法通路;两重复点(标为蓝黑色)兼有二部的性质,因此黑色和蓝色(包括自身)均可连通。化为有向边,得到

所以得到两条合法路径:

附录
-
#include <bits/stdc++.h>using namespace std;queue<int> open; // 存放还未使用的数字 int Q[10] = {0}; // 九宫格void myPrint() {for (int i = 1; i < 10; i++){printf("%d%c", Q[i], i % 3 == 0 ? '\n' : ' ');}cout << endl; }void dfs(int n) // n:在九宫格中的目标放置位置 {if (n == 10)// 九宫格已被填满{int flag = 1;// 分别验证三行for (int i = 0; i < 3; i++){int sum = 0; // 行和for (int j = 1; j <= 3; j++){sum = sum * 10 + Q[i * 3 + j];}if ((int)sqrt(sum) * (int)sqrt(sum) != sum){flag = 0;break;}}if (flag == 1){myPrint();}}else{// 逐个将open中的元素在第n位尝试for (int i = 1; i <= (10 - n); i++){int tmp = open.front();Q[n] = tmp;open.pop();dfs(n + 1);open.push(tmp);}}return; }int main() {for (int i = 1; i <= 9; i++){open.push(i);}dfs(1); // 从第一个位置开始dfsreturn 0; }
1; i <= 9; i++)
{
open.push(i);
}
dfs(1); // 从第一个位置开始dfs
return 0;
}