问题本质:联通体面积
深搜简略版描述: 没有出口, 能走就走, 累加递归的结果。
广搜简略版描述:不断拓展新边界,累加后入队。
例题参考:迷雾森林、红与黑 这里举迷雾森林的例子(90%参考y总)
描述
迷雾森林被加农的玷污了,原本圣洁无比的迷雾森林,如今被彻底玷污,空气中充满着紫色的恶臭。
林克临危不惧,带上呼吸面罩,挥舞大师之剑的光芒,净化迷雾。林克所到之处,加农褪去,圣洁回归。
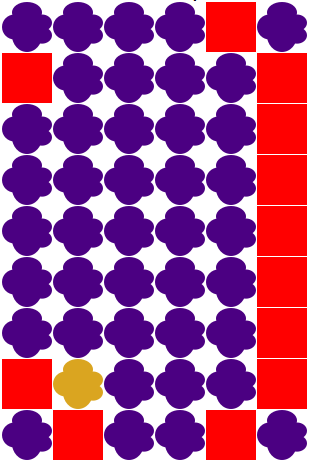
如下图,红色代表墙壁,紫色的迷雾代表需要净化的空间,金色代表林克开始净化的起点。
从某处开始,林克只能向相邻的紫色区域移动。请问,林克总共能够净化多少区域?
图1 初始状态 图2 净化中.....
-----
输入
包括多个数据集合。每个数据集合的第一行是两个整数W和H,分别表示x方向和y方向瓷砖的数量。W和H都不超过20。
在接下来的H行中,每行包括W个字符。
每个字符表示一个区域的状态,规则如下
1)‘.’:代表紫色迷雾

;
2)‘#’:代表红墙

;
3)‘@’:代表林克的起始位置

(该字符在每个数据集合中唯一出现一次。)
当在一行中读入的是两个零时,表示输入结束。
输出
对每个数据集合,分别输出一行,显示林克从初始位置出发能净化的迷雾数(记数时包括初始位置的迷雾)。
输入样例 1
6 9 ....#. .....# ...... ...... ...... ...... ...... #@...# .#..#. 0 0
输出样例 1
45
深搜写法:优点:简单代码少 缺点:数据大有爆栈的风险
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;typedef long long LL;const int N = 35;
bool st[N][N];
char g[N][N];
int w, h;
int dx[] = {-1, 0, 1, 0}, dy[] = {0, 1, 0, -1};int dfs(int x, int y){int cnt = 1;st[x][y] = true;for(int i = 0; i < 4; ++ i){int nx = x + dx[i], ny = y + dy[i];// cout << nx << ny << endl; if(nx < 0 || nx >= h || ny < 0 || ny >= w) continue; //出界if(st[nx][ny]) continue; //走过 if(g[nx][ny] == '#') continue; //墙壁cnt += dfs(nx, ny); //累加// cout << cnt << endl;}return cnt;
}int main(){while(cin >> w >> h, w || h){for(int i = 0; i < h; ++ i) cin >> g[i];int x, y;for(int i = 0; i < h; ++ i)for(int j = 0; j < w; ++ j){if(g[i][j] == '@'){x = i; y = j; //标记出发点}}cout << dfs(x, y) << endl;memset(st, 0, sizeof st);}return 0;
}
广搜写法: 1.优点:没有爆栈的风险,运行更优 2.缺点:要建个队列,写起来麻烦一点
//联通体
#include<iostream>
#include<queue>
#include<cstring>
using namespace std;#define x first
#define y secondtypedef pair<int, int> PII; //因为要入队 所以一起存比较方便const int N = 25;
char g[N][N];
int w, h, res = 1;
bool st[N][N];int bfs(PII start){queue<PII> q;q.push(start);st[start.x][start.y] = true;int dx[] = {-1, 0, 1, 0}, dy[] = {0, 1, 0, -1};while(q.size()){ //Flood fill算法 不断拓展新边界PII tmp = q.front();q.pop();for(int i = 0; i < 4; ++ i){int x = tmp.x + dx[i], y = tmp.y + dy[i];if(x >= h || x < 0 || y >= w || y < 0) continue;if(g[x][y] == '#') continue;if(st[x][y]) continue;++ res;st[x][y] = true;q.push({x, y});}}return res;
}int main(){while(cin >> w >> h && w || h){ //非0输入res = 1; memset(st, false, sizeof st);for(int i = 0; i < h; ++ i) cin >> g[i];PII start;for(int i = 0; i < h; ++ i){for(int j = 0; j < w; ++ j){if(g[i][j] == '@') start = {i, j};}}cout << bfs(start) << endl;
}return 0;
}