Numerical optimization拟牛顿法DFP python实现

引入包

from scipy.optimize import minimize
from numpy import *
import numpy
import numpy as npimport scipy

求解$Bp=?g$

def newton_point(g,B):cho_info = scipy.linalg.cho_factor(B)newton_point = -scipy.linalg.cho_solve(cho_info, g)return newton_point  ## 标题

定义凸优化问题：

def f(x):return 0.5*np.dot(np.dot(x,A),x)+np.dot(b,x)+c
def  g(x):return np.dot(A,x)+b
def minimize_bfgs(f, x0, jac=None,gtol=1e-5,disp=False):

DFP 算法实现：

    # 第一步，给出初始点x0, Ho, 计算gogfk = g(x0)k = 0N = len(x0)I = numpy.eye(N, dtype=int)Bk = I# 初始化Hessian 矩阵xk = x0# 初始时方向为最速下降方向gnorm = numpy.amax(numpy.abs(gfk))while (gnorm > gtol):# 第二步 ： 求下降方向# pk = -numpy.dot(Hk, gfk) pk=newton_point(gfk,Bk)# 第三步： 这里使用了精确线搜索确定步长，并更新xk+1alpha_k = -np.dot(pk.T, g(xk))/np.dot(pk.T,np.dot(A,pk))xkp1 = xk + alpha_k * pk# 第四步： 校正Bksk = xkp1 - xkxk = xkp1gfkp1 = g(xkp1)yk = gfkp1 - gfkgfk = gfkp1k += 1gnorm = numpy.amax(numpy.abs(gfk))if (gnorm <= gtol):breakrhok = 1.0 / (numpy.dot(yk, sk))A1= I - yk[:, None] *sk[None, :] * rhokA2 = I - sk[:, None] * yk[None, :] * rhokBk = np.dot(np.dot(A1, Bk),A2 ) + rhok * sk[:,None]*sk[None,:]print(" Current function value xk:[%f %f]"% (xk[0],xk[1]))print(" Current function value: %f" % f(xk))print("BK",Bk)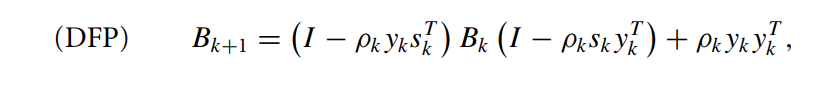

测试

f __name__ == '__main__':# x0 = [2, 1]# A=np.array([[4,1],[2,5]])# b=[-1,2]# c=0# g0=g(x0)print(minimize_bfgs(f, x0, jac=g,gtol=1e-6, disp= True))res = minimize(f, x0, method='BFGS', jac=g, options={
    'gtol': 1e-6, 'disp': True})print(res)