用于求解线性规划的原始-对偶对数障碍函数法在信号分解和压缩感知中的应用

内点法

\quad单纯形法$（SimplexMethod）$可以用来求解带约束的线性规划命题$（LP）$，与之类似的有效集法$（ActiveSetMethod）$可以用来求解带约束的二次规划$（QP）$，而内点法$（InteriorPointMethod）$则是另一种用于求解带约束的优化命题的方法。而且无论是面对$LP$还是$QP$，内点法都显示出了相当的极好的性能，例如多项式的算法复杂度。内点法主要有障碍函数法$（BarrierMethod）$和原始对偶法$（Primal?DualMethod）$。
本文中采用由$Donoho$等人发表在论文$Atomic$ $Decomposition$ $by$ $Basis$ $Pursuit$中提出的原始$?$对偶对数障碍函数法。该论文利用原始$?$对偶对数障碍函数法和共轭梯度法成功求解了大规模的优化问题。

原始$?$对偶对数障碍函数法

\quad本文中主要利用原始$?$对偶对数障碍函数法来求解下面的一个带扰动的线性规划问题，也可以理解为二次规划问题。
$$\underset{x}{\min }{c}^{T}x+\frac{1}{2}{\Vert \gamma x\Vert }^2+\frac{1}{2}{\Vert p\Vert }^2\mathrm{s}.\mathrm{t}.Ax+\sigma p=bx\ge 0$$
$p$是一个高斯白噪声，$\sigma$是扰动的水平，$\gamma$是$x$的扰动。论文中$\gamma$代表扰动，也可以理解为范数。下面是原始$?$对偶对数障碍函数法算法：


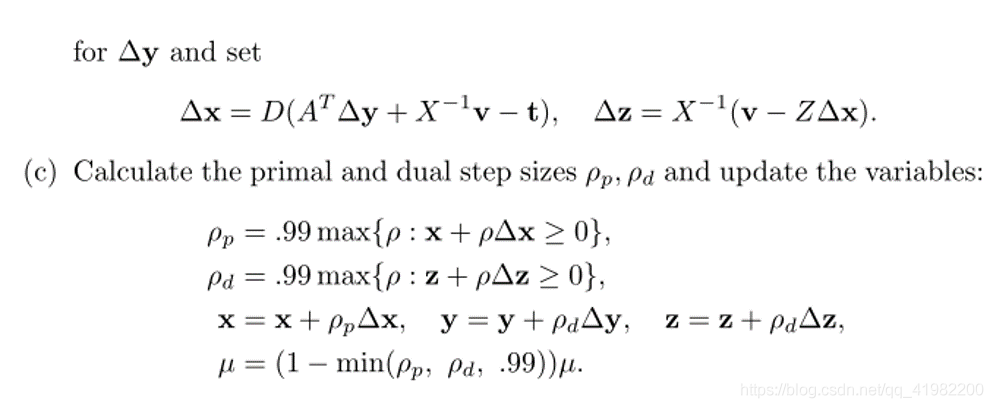
如果对该算法感兴趣，可以浏览最后两篇参考文献，特别是第三篇参考文献给出了更一般的二次规划算法。

信号分解中的应用

上述参数设置不同的值，会有下面两个不同的模型。
$$(MOF)\min {\Vert x\Vert }_2\mathrm{s}.\mathrm{t}.y=Axx\ge 0$$

$$(BPDN)\mathrm{m}\mathrm{i}\mathrm{n}{\Vert x\Vert }_1\mathrm{s}.\mathrm{t}.Ax=yx\ge 0$$
上述两个模型都是为了实现信号的自动分解，$MOF$存在两个问题：
$(1)$分解出来的系数不稀疏。在某些情况下，如果信号本身就具有稀疏性，这样分解出来的结果就会非常糟糕。
$(2)$$MOF$本身存在分辨率受限的问题。
$BPDN$就是把$BP$基追踪应用于去噪，所以命名。相比于$MOF$，$BPDN$把$2$范数变为$1$范数，这就可以保持稀疏性。
但是前者的运算速度会远远快于后者。尽管利用下面的程序，可能会得出完全相反的结论。这主要是利用原始$?$对偶对数障碍函数法算法去实现$MOF$并不是明智的选择。后面，我会写关于$MOF$该算法的程序。

压缩感知中的应用

\quad在这里，我么将$BPDN$模型，也就是$BP$应用于压缩感知$CS$恢复重建过程。我们使用高斯随机矩阵作为测量矩阵$A$，稀疏度$K=10$,原始信号是一个只有$K$个为$1$，其余为$0$的信号。也就相当于信号分解中的一个过完备字典。那么只要$\sigma =0$，$\gamma =0$，$c$是一个全$1$的列向量即可。

算法程序

function [x,z] = PDLB_LP(c,A,b,delta,gama)
%UNTITLED5 此处显示有关此函数的摘要
%   此处显示详细说明
%A Primal-Dual Log-Barrier LP Algorithm
%set parameters
FeaTol=1e-4;%the feasibility tolerance 
PDGapTol=1e-4;%the duality gap tolerance
% delta=0.01;%delta=1，即为BPDN,delta也可以为1e-4
% gama=0.01;%gama,原始变量的扰动
%Initialize
[m,n]=size(A);
x=ones(n,1);%生成全1向量
y=zeros(m,1);%生成全0向量
z=0.5*ones(n,1);
e=ones(n,1);
miu=1;
%Loop
t=c+(gama^2)*x-z-A'*y;
r=b-A*x-(delta^2)*y;
X=diag(x,0);%生成对角线元素为x的对角矩阵
Z=diag(z,0);
v=miu*e-Z*x;
%step a
D=inv(X\Z+(gama^2)*eye(n));%A\b=inv(A)*b
PInfeas=norm(r,2)/(1+norm(x,2));%Primal infeasibility
DInfeas=norm(t,2)/(1+norm(y,2));%Dual infeasibility
DuGap=(z'*x)/(1+norm(x,2)*norm(z,2));
while(PInfeas>FeaTol || DInfeas>FeaTol || DuGap>PDGapTol)%step b:solveif (delta>0)A1=[(D^(1/2))*A';delta*eye(m)];%(n+m,m)B=[(D^(1/2))*(t-X\v);r/delta];y1=pinv(A1)*B;%广义逆，最小二次法求delta_y,即y1elsey1=(A*D*A')\(r+A*D*(t-X\v));endx1=D*(A'*y1+X\v-t);z1=X\(v-Z*x1);%step c:Calculate the primal and dual step sizes ρp,ρd and update the variables:index1=find(x1<0);index2=find(z1<0);if isempty(index1)==0 && isempty(index2)==0%不是空x2=x1(index1);%储存负数z2=z1(index2);x3=x(index1);%储存x1中负数对应的x值z3=z(index2);p1=abs(x3./x2);p2=abs(z3./z2);elseif isempty(index1)==0 && isempty(index2)==1x2=x1(index1);%储存负数x3=x(index1);%储存x1中负数对应的x值p1=abs(x3./x2);p2=p1;elseif isempty(index1)==1 && isempty(index2)==0z2=x1(index2);%储存负数z3=z(index2);%储存x1中负数对应的x值p2=abs(z3./z2);p1=p2;elsep1=min(x./x1);p2=min(z./z1);endrou_p=0.99*min(p1);rou_d=0.99*min(p2);x=x+rou_p*x1;y=y+rou_d*y1;z=z+rou_d*z1;miu=(1-min([rou_p,rou_d,0.99]))*miu;%step at=c+(gama^2)*x-z-A'*y;r=b-A*x-(delta^2)*y;X=diag(x,0);%生成对角线元素为x的对角矩阵Z=diag(z,0);v=miu*e-Z*x;D=inv(X\Z+(gama^2)*eye(n));%A\b=inv(A)*bPInfeas=norm(r,2)/(1+norm(x,2));%Primal infeasibilityDInfeas=norm(t,2)/(1+norm(y,2));%Dual infeasibilityDuGap=(z'*x)/(1+norm(x,2)*norm(z,2));
end
end

实验结果

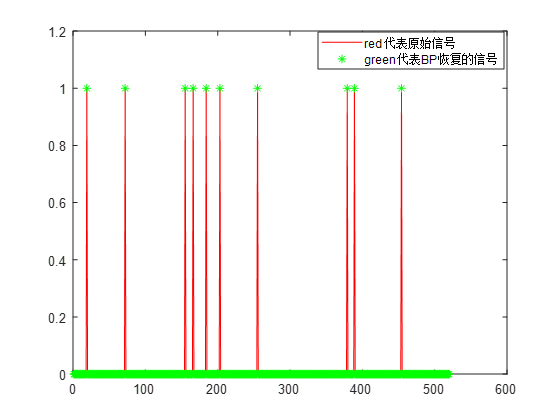
https://blog.csdn.net/dymodi/article/details/46441783
Chen S S , Saunders D M A . Atomic Decomposition by Basis Pursuit[J]. Siam Review, 2001, 43(1):129-159.
P. E. Gill, W. Murray, D. B. Ponceleón, and M. A. Saunders, Solving Reduced KKT Systems in Barrier Methods for Linear and Quadratic Programming, Report SOL 91-7, Stanford University, Stanford, CA, July 1991.