题解思路及源码,来自 蓝桥杯 郑未老师。
目 录
一、世纪末的星期
二、马虎的算式
三、振兴中华
四、黄金连分数
Decimal用法
五、有理数类
六、三部排序
七、错误票据
八、幸运数
九、带分数
全排列模板——整数数组
十、连号区间数
小结
一、世纪末的星期
标题: 世纪末的星期
曾有邪教称1999年12月31日是世界末日。当然该谣言已经不攻自破。
还有人称今后的某个世纪末的12月31日,如果是星期一则会....
有趣的是,任何一个世纪末的年份的12月31日都不可能是星期一!!
于是,“谣言制造商”又修改为星期日......
1999年的12月31日是星期五,请问:未来哪一个离我们最近的一个世纪末年(即xx99年)的12月31日正好是星期天(即星期日)?
请回答该年份(只写这个4位整数,不要写12月31等多余信息)
【解析】:此题使用java中的日历类
【答案】:2299

package provincialGames_04_2013;import java.util.Calendar;public class A01_世纪末的星期 { //可用Excel解答 = WEEKDAY(A1,2)public static void main(String[] args) {Calendar calendar = Calendar.getInstance(); //获取Calendar类的实例for(int year = 1999; year < 10000; year += 100) {calendar.set(Calendar.YEAR, year); //set()方法 两个参数【设置的项,设置的值】calendar.set(Calendar.MONTH, 11); // 从0开始计数。1月是0, 12月是11calendar.set(Calendar.DAY_OF_MONTH, 31); //设置日期 31号System.out.println(year + " " + calendar.get(Calendar.DAY_OF_WEEK)); //验证1999年12月31日 星期五 是不是 6if(calendar.get(Calendar.DAY_OF_WEEK) == 1) { //get()方法 获取 值; DAY_OF_WEEK一周中的第几天,星期日是第一天System.out.println(year);break;}}}}
//按Ctrl键 关联 源码 , 385行:一月份 是 0
calendar.set(Calendar.YEAR, year);//设置12月
calendar.set(Calendar.MONTH, 11);//442 The first day of the month has value 1.
calendar.set(Calendar.DAY_OF_MONTH, 31);if(calendar.get(Calendar.DAY_OF_WEEK) == 1) {//456行
System.out.println(year);
break;
}日 1
一 2
二 3
三 4
四 5
五 6
六 7String s = new SimpleDateFormat("yyyy-MM-dd").format(getLastDay(2017, 9));
二、马虎的算式
B组第2题
C组第3题标题: 马虎的算式
小明是个急性子,上小学的时候经常把老师写在黑板上的题目抄错了。
有一次,老师出的题目是:36 x 495 = ?
他却给抄成了:396 x 45 = ?
但结果却很戏剧性,他的答案竟然是对的!!
因为 36 * 495 = 396 * 45 = 17820
类似这样的巧合情况可能还有很多,比如:27 * 594 = 297 * 54
假设 a b c d e 代表1~9不同的5个数字(注意是各不相同的数字,且不含0)
能满足形如: ab * cde = adb * ce 这样的算式一共有多少种呢?
请你利用计算机的优势寻找所有的可能,并回答不同算式的种类数。满足乘法交换律的算式计为不同的种类,所以答案肯定是个偶数。
答案直接通过浏览器提交。
注意:只提交一个表示最终统计种类数的数字,不要提交解答过程或其它多余的内容。
/*假设 a b c d e 代表1~9不同的5个数字(注意是各不相同的数字,且不含0)
能满足形如: ab * cde = adb * ce 这样的算式一共有多少种呢?*/
【解析】:暴力穷举即可
【答案】:142

package provincialGames_04_2013;public class A02_马虎的算式 {public static void main(String[] args) {int ans = 0;for(int a = 1; a < 10; a++) {for(int b = 1; b < 10; b++) {if(b != a) for(int c = 1; c < 10; c++) {if(c != a && c != b) for(int d = 1; d < 10; d++) {if(d != a && d != b && d != c) for(int e = 1; e < 10; e++) {if(e != a && e != b && e != c && e != d && e != d) {if((a*10+b)*(c*100+d*10+e) == (a*100+d*10+b)*(c*10+e)) {ans++;//System.out.printf("(%d*10+%d)*(%d*100+%d*10+%d) == (%d*100+%d*10+%d)*(%d*10+%d)\n", a, b, c, d, e, a, d, b, c, e);}}}}}}}System.out.println(ans);}}
package provincialGames_04_2013;public class A02_马虎的算式2 {public static void main(String[] args) {int sum=0;for(int a = 1; a < 10; a++)for(int b = 1; b < 10; b++)for(int c = 1; c < 10; c++)for(int d = 1; d < 10; d++)for(int e = 1; e < 10; e++)if(a != b && a != c && a != d && a != e && b != c && b != d && b != e && c != d && c != e && d != e)if((a*10+b)*(c*100+d*10+e) == (a*100+d*10+b)*(c*10+e)) sum++;System.out.println(sum);}}
三、振兴中华
标题: 振兴中华
小明参加了学校的趣味运动会,其中的一个项目是:跳格子。
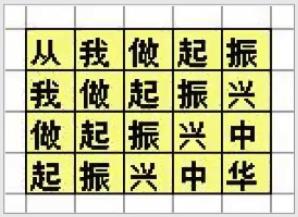
地上画着一些格子,每个格子里写一个字,如下所示:(也可参见p1.jpg)从我做起振
我做起振兴
做起振兴中
起振兴中华比赛时,先站在左上角的写着“从”字的格子里,可以横向或纵向跳到相邻的格子里,但不能跳到对角的格子或其它位置。一直要跳到“华”字结束。
要求跳过的路线刚好构成“从我做起振兴中华”这句话。
请你帮助小明算一算他一共有多少种可能的跳跃路线呢?
答案是一个整数,请通过浏览器直接提交该数字。
注意:不要提交解答过程,或其它辅助说明类的内容。
从我做起振 (0, 0) (0, 1) (0, 2) (0, 3) (0, 4)
我做起振兴 (1, 0) (1, 1) (1, 2) (1, 3) (1, 4)
做起振兴中 (2, 0) (2, 1) (2, 2) (2, 3) (2, 4)
起振兴中华 (3, 0) (3, 1) (3, 2) (3, 3) (3, 4)
【解析】:将格子中的字存放到一个二维数组中,使用回溯法依次进行遍历,
符合条件的+1,最后求出总和【答案】:35

递归:走梯子
f(n) = f(n - 1) + f(n - 2)
重复解 重叠子问题
记忆性递归
动态规划
package provincialGames_04_2013;public class A03_振兴中华 {public static void main(String[] args) {/**重复、变化、边界向下或向右走,才有意义x == 4 || y == 3 只有一种解法 */int ans = f(0, 0);System.out.println(ans);}public static int f(int x, int y) {if(x == 4 || y == 3) {return 1;}return f(x+1, y) + f(x, y+1); // 将两种走法的路线数相加}
}
四、黄金连分数
标题: 黄金连分数
黄金分割数0.61803... 是个无理数,这个常数十分重要,在许多工程问题中会出现。有时需要把这个数字求得很精确。
对于某些精密工程,常数的精度很重要。也许你听说过哈勃太空望远镜,它首次升空后就发现了一处人工加工错误,对那样一个庞然大物,
其实只是镜面加工时有比头发丝还细许多倍的一处错误而已,却使它成了“近视眼”!!
言归正传,我们如何求得黄金分割数的尽可能精确的值呢?有许多方法。比较简单的一种是用连分数:
1
黄金数 = ---------------------
1
1 + -----------------
1
1 + -------------
1
1 + ---------
1 + ...
这个连分数计算的“层数”越多,它的值越接近黄金分割数。请你利用这一特性,求出黄金分割数的足够精确值,要求四舍五入到小数点后100位。
小数点后3位的值为:0.618
小数点后4位的值为:0.6180
小数点后5位的值为:0.61803
小数点后7位的值为:0.6180340
(注意尾部的0,不能忽略)你的任务是:写出精确到小数点后100位精度的黄金分割值。
注意:尾数的四舍五入! 尾数是0也要保留!
显然答案是一个小数,其小数点后有100位数字,请通过浏览器直接提交该数字。
注意:不要提交解答过程,或其它辅助说明类的内容。
//1.化为求斐波那契相邻两项的比值,到多少项?越多越精确,n/n+1项,n再往上增加,这个比值的小数点后101位是稳定的,也就是不变的
//2.double无法表示100位小数,BigInteger和BigDecimal【答案】:0.6180339887498948482045868343656381177203091798057628621354486227052604628189024497072072041893911375

package provincialGames_04_2013;import java.math.BigDecimal;
import java.math.BigInteger;public class A04_黄金连分数 {public static void main(String[] args) {BigInteger a = BigInteger.ONE;BigInteger b = BigInteger.ONE;//斐波那契的迭代形式for (int i = 3; i < 500; i++) { //200 300 400 500BigInteger t = b;b = a.add(b); //大整数加法a = t;}//new BigDecimal(a, 110) 将整数转为BigDecimal 指定一个精确度 【长度 110】//大浮点数的除法BigDecimal divide = new BigDecimal(a, 110).divide(new BigDecimal(b, 110), BigDecimal.ROUND_HALF_DOWN);System.out.println(divide.toPlainString().substring(0, 103)); //[0, 102] 共103个字符 字符串分割(截取)//ROUND_HALF_DOWN:五舍六入 ; toPlainString() 与 toString() 用法相似}}
1 1/(1+1) 1/(1+1/(1+1)) ...
1 1/2 2/3 3/5 5/8 8/13 ...1 1 2 3 5 8 13 21 34 55 ... 斐波那契数列
答案:相邻的两项斐波那契数列之比。
不能用double,double表示不了太多位。
// System.out.println("abcdefg".substring(0, 4)); //[0, 3] abcd
// Scanner sc = new Scanner(System.in);
// String str = sc.next();
// System.out.println(str.length());
java.math.BigDecimal.valueOf()方法的声明
public static BigDecimal valueOf(double val)
参数: val - double转换为一个BigDecimal。
返回值: 此方法返回一个BigDecimal,其值等于或约等于val的值。
异常: NumberFormatException - 如果val为无穷或NaN
i < 200 :
0.61803398874989484820458683436563811772030917980576286213544862270526046281890244969233401224637257135【长度:103位】
i < 300 :
0.61803398874989484820458683436563811772030917980576286213544862270526046281890244970720720418939113748【长度:103位】
i < 400 :
0.61803398874989484820458683436563811772030917980576286213544862270526046281890244970720720418939113748【长度:103位】
【i < 300】 ---> 【i < 400】 ---> 【i < 500】 :300、400、500输出没有变化i < 500 :
0.61803398874989484820458683436563811772030917980576286213544862270526046281890244970720720418939113748【长度:103位】小数点后共101位
0.6180339887498948482045868343656381177203091798057628621354486227052604628189024497072072041893911375【102位---答案】
BigDecimal(BigInteger unscaledVal, int scale)
这个构造函数用于转换为BigInteger非标度值和一个int尺度成一个BigDecimal。System.out.println("abcde".subSequence(0, 3)); //abc [start, end-1]
System.out.println("abcde".substring(0, 3)); //abc [start, end-1]
Decimal用法
package provincialGames_04_2013;import java.math.BigDecimal;public class A04_Decimal用法 {public static void main(String[] args) {//使用toString() --> 不改变输出BigDecimal bg;Long l = new Long("12345678");bg = BigDecimal.valueOf(l, 4);System.out.println( bg );System.out.println("new BigDecimal(0.99): " + new BigDecimal(0.99));System.out.println("new BigDecimal(0.99).toString(): " + new BigDecimal(0.99).toString());System.out.println("new BigDecimal(\"0.99\"): " + new BigDecimal("0.99"));System.out.println("new BigDecimal(\"0.99\").toString(): " + new BigDecimal("0.99").toString());System.out.println("BigDecimal.valueOf(0.99): " + BigDecimal.valueOf(0.99));System.out.println("BigDecimal.valueOf(0.99f): " + BigDecimal.valueOf(0.99f));System.out.println("new BigDecimal(Double.toString(0.99)).toString(): " + new BigDecimal(Double.toString(0.99)).toString());System.out.println("BigDecimal.valueOf(1.234).setScale(2,BigDecimal.ROUND_HALF_DOWN)="+BigDecimal.valueOf(1.234).setScale(2,BigDecimal.ROUND_HALF_DOWN));System.out.println("BigDecimal.valueOf(1.235).setScale(2,BigDecimal.ROUND_HALF_DOWN)="+BigDecimal.valueOf(1.235).setScale(2,BigDecimal.ROUND_HALF_DOWN));System.out.println("BigDecimal.valueOf(1.236).setScale(2,BigDecimal.ROUND_HALF_DOWN)="+BigDecimal.valueOf(1.236).setScale(2,BigDecimal.ROUND_HALF_DOWN));System.out.println("BigDecimal.valueOf(1.234).setScale(2,BigDecimal.ROUND_HALF_UP)="+BigDecimal.valueOf(1.234).setScale(2,BigDecimal.ROUND_HALF_UP));System.out.println("BigDecimal.valueOf(1.235).setScale(2,BigDecimal.ROUND_HALF_UP)="+BigDecimal.valueOf(1.235).setScale(2,BigDecimal.ROUND_HALF_UP));System.out.println("BigDecimal.valueOf(1.236).setScale(2,BigDecimal.ROUND_HALF_UP)="+BigDecimal.valueOf(1.236).setScale(2,BigDecimal.ROUND_HALF_UP));BigDecimal bbb = new BigDecimal(0.4321);System.out.println(bbb.toPlainString());System.out.println(bbb.toString());}/*** 提供精确的加法运算** @param v1 被加数* @param v2 加数* @param scale 保留scale 位小数* @return 两个参数的和*/public static String add(String v1, String v2, int scale) {if (scale < 0) {throw new IllegalArgumentException("保留的小数位数必须大于零");}BigDecimal b1 = new BigDecimal(v1);BigDecimal b2 = new BigDecimal(v2);return b1.add(b2).setScale(scale, BigDecimal.ROUND_HALF_UP).toString();}/*** 提供精确的减法运算** @param v1 被减数* @param v2 减数* @param scale 保留scale 位小数* @return 两个参数的差*/public static String sub(String v1, String v2, int scale) {if (scale < 0) {throw new IllegalArgumentException("保留的小数位数必须大于零");}BigDecimal b1 = new BigDecimal(v1);BigDecimal b2 = new BigDecimal(v2);return b1.subtract(b2).setScale(scale, BigDecimal.ROUND_HALF_UP).toString();}/*** 提供精确的乘法运算** @param v1 被乘数* @param v2 乘数* @param scale 保留scale 位小数* @return 两个参数的积*/public static String mul(String v1, String v2, int scale) {if (scale < 0) {throw new IllegalArgumentException("保留的小数位数必须大于零");}BigDecimal b1 = new BigDecimal(v1);BigDecimal b2 = new BigDecimal(v2);return b1.multiply(b2).setScale(scale, BigDecimal.ROUND_HALF_UP).toString();}/*** 提供精确的除法运算。当发生除不尽的情况时,由scale参数指定精度,以后的数字四舍五入** @param v1 被除数* @param v2 除数* @param scale 表示需要精确到小数点以后几位* @return 两个参数的商*/public static String div(String v1, String v2, int scale) {if (scale < 0) {throw new IllegalArgumentException("保留的小数位数必须大于零");}BigDecimal b1 = new BigDecimal(v1);BigDecimal b2 = new BigDecimal(v2);return b1.divide(b2, scale, BigDecimal.ROUND_HALF_UP).toString();}/*** 提供精确的小数位四舍五入处理** @param v 需要四舍五入的数字* @param scale 小数点后保留几位* @return 四舍五入后的结果*/public static double round(double v, int scale) {if (scale < 0) {throw new IllegalArgumentException("保留的小数位数必须大于零");}BigDecimal b = new BigDecimal(Double.toString(v));return b.setScale(scale, BigDecimal.ROUND_HALF_UP).doubleValue();}/*** 取余数** @param v1 被除数* @param v2 除数* @param scale 小数点后保留几位* @return 余数*/public static String remainder(String v1, String v2, int scale) {if (scale < 0) {throw new IllegalArgumentException("保留的小数位数必须大于零");}BigDecimal b1 = new BigDecimal(v1);BigDecimal b2 = new BigDecimal(v2);return b1.remainder(b2).setScale(scale, BigDecimal.ROUND_HALF_UP).toString();}/*** 比较大小** @param v1 被比较数* @param v2 比较数* @return 如果v1 大于v2 则 返回true 否则false*/public static boolean compare(String v1, String v2) {BigDecimal b1 = new BigDecimal(v1);BigDecimal b2 = new BigDecimal(v2);int bj = b1.compareTo(b2);if (bj > 0)return true;elsereturn false;}}
/**
valueOf() 方法用于返回给定参数的原生 Number 对象值,参数可以是原生数据类型, String等。
该方法是静态方法。该方法可以接收两个参数一个是字符串,一个是基数。Integer valueOf(int i):返回一个表示指定的 int 值的 Integer 实例。Integer valueOf(String s):返回保存指定的 String 的值的 Integer 对象。Integer valueOf(String s, int radix): 返回一个 Integer 对象,
该对象中保存了用第二个参数提供的基数进行解析时从指定的 String 中提取的值。Integer b = Integer.valueOf("444",16); // 使用 16 进制BigDecimal.valueof(Double t)与BigDecimal.valueof(String t) : 第二个 不会输出 多余的值Java中提供了大数字(超过16位有效位)的操作类,即 java.math.BinInteger 类和 java.math.BigDecimal 类,用于高精度计算.其中 BigInteger 类是针对大整数的处理类,而 BigDecimal 类则是针对大小数的处理类.BigDecimal 类的实现用到了 BigInteger类,不同的是 BigDecimal 加入了小数的概念.float和Double只能用来做科学计算或者是工程计算;在商业计算中,对数字精度要求较高,必须使用 BigInteger 类和 BigDecimal 类,它支持任何精度的定点数,可以用它来精确计算货币值.BigDecimal类创建的是对象,不能使用传统的+、-、*、/等算术运算符直接对其进行数学运算,而必须调用其对应的方法.方法的参数也必须是BigDecimal类型的对象.一、构造BigDecimal 对象常用方法1、方法一
BigDecimal BigDecimal(double d); //不允许使用2、方法二
BigDecimal BigDecimal(String s); //常用,推荐使用3、方法三
static BigDecimal valueOf(double d); //常用,推荐使用注意:1. double 参数的构造方法,不允许使用!!!!因为它不能精确的得到相应的值,值会变大;2. String 构造方法是完全可预知的: 写入 new BigDecimal("0.1") 将创建一个 BigDecimal,它正好等于预期的0.1; 因此,通常建议优先使用 String 构造方法;3. 静态方法 valueOf(double val) 内部实现,仍是将 double 类型转为 String 类型; 这通常是将 double(或float)转化为 BigDecimal 的首选方法;BigDecimal.ROUND_HALF_DOWN最贴切的说法应该是叫五舍六入,舍弃的部分如果大于5才进位,小于或等于5直接舍弃。BigDecimal.ROUND_HALF_UP就是我们小学教的四舍五入,舍弃的部分如果大于等于5就进位,小于5的直接舍弃。
*/
package provincialGames_04_2013;import java.math.BigDecimal;
import java.math.BigInteger;public class A04_Decimal用法2 {public static void main(String[] args) {BigInteger a = BigInteger.ONE;BigDecimal b = new BigDecimal(a, 5);System.out.println(b);System.out.println("abcde".subSequence(0, 3)); //abc [start, end-1]System.out.println("abcde".substring(0, 3)); //abc [start, end-1]}}
五、有理数类
同时是C组第5题
标题:有理数类
有理数就是可以表示为两个整数的比值的数字。一般情况下,我们用近似的小数表示。但有些时候,不允许出现误差,必须用两个整数来表示一个有理数。
这时,我们可以建立一个“有理数类”,下面的代码初步实现了这个目标。为了简明,它只提供了加法和乘法运算。
class Rational
{
private long ra;
private long rb;private long gcd(long a, long b){
if(b==0) return a;
return gcd(b,a%b);
}
public Rational(long a, long b){
ra = a;
rb = b;
long k = gcd(ra,rb);
if(k>1){ //需要约分
ra /= k;
rb /= k;
}
}
// 加法
public Rational add(Rational x){
return ________________________________________; //填空位置
}
// 乘法
public Rational mul(Rational x){
return new Rational(ra*x.ra, rb*x.rb);
}
public String toString(){
if(rb==1) return "" + ra;
return ra + "/" + rb;
}
}使用该类的示例:
Rational a = new Rational(1,3);
Rational b = new Rational(1,6);
Rational c = a.add(b);
System.out.println(a + "+" + b + "=" + c);
请分析代码逻辑,并推测划线处的代码,通过网页提交
注意:仅把缺少的代码作为答案,千万不要填写多余的代码、符号或说明文字!!
【答案】:Rational(this.ra*x.rb + this.rb*x.ra, this.rb*x.rb)

package provincialGames_04_2013;public class A05_有理数类 {static class Rational //内部类 【main调用内部类 : 内部类前 要加 static】{private long ra;private long rb;private long gcd(long a, long b){ //辗转相除法 求 最大公约数gcdif(b==0) return a;return gcd(b,a%b);}public Rational(long a, long b){ra = a;rb = b; long k = gcd(ra,rb);if(k>1){ //需要约分ra /= k; rb /= k;}}// 加法public Rational add(Rational x){return new Rational(this.ra*x.rb + this.rb*x.ra, this.rb*x.rb); //填空位置// 一定返回Rational 所以, 先new一个Rational// 分母:分母*分母:this.rb*x.rb// 分子:自己的分子*x的分母+自己的分母*x的分子}// 乘法public Rational mul(Rational x){return new Rational(ra*x.ra, rb*x.rb); //更新 分子与分母:分子*分子、分母*分母}public String toString(){if(rb==1) return "" + ra;return ra + "/" + rb;}}public static void main(String[] args) {Rational a = new Rational(1,3);Rational b = new Rational(1,6);Rational c = a.add(b);System.out.println(a + "+" + b + "=" + c);}}
六、三部排序
标题:三部排序
一般的排序有许多经典算法,如快速排序、希尔排序等。
但实际应用时,经常会或多或少有一些特殊的要求。我们没必要套用那些经典算法,可以根据实际情况建立更好的解法。
比如,对一个整型数组中的数字进行分类排序:
使得负数都靠左端,正数都靠右端,0在中部。注意问题的特点是:负数区域和正数区域内并不要求有序。可以利用这个特点通过1次线性扫描就结束战斗!!
以下的程序实现了该目标。
static void sort(int[] x)
{
int p = 0;
int left = 0;
int right = x.length-1;while(p<=right){
if(x[p]<0){
int t = x[left];
x[left] = x[p];
x[p] = t;
left++;
p++;
}
else if(x[p]>0){
int t = x[right];
x[right] = x[p];
x[p] = t;
right--;
}
else{
_________________________; //代码填空位置
}
}
}如果给定数组:
25,18,-2,0,16,-5,33,21,0,19,-16,25,-3,0
则排序后为:
-3,-2,-16,-5,0,0,0,21,19,33,25,16,18,25请分析代码逻辑,并推测划线处的代码,通过网页提交
注意:仅把缺少的代码作为答案,千万不要填写多余的代码、符号或说明文字!!
【答案】:p++

快速排序:单指针扫描、双指针扫描、三指针扫描(重复元素多)
package provincialGames_04_2013;public class A06_三部排序 { // 负数都靠左端,正数都靠右端,0在中部static void sort(int[] x) //解题技巧:边猜测、边验证、逐步推理逻辑//极限思维 全是0 --> p++ //填空题:一般就一行代码{int p = 0;int left = 0; // 下标int right = x.length-1; // 最大下标while(p<=right){if(x[p]<0){ //left的左侧,全部<0//元素<0, 将元素与left位置元素 互换int t = x[left];x[left] = x[p];x[p] = t;left++;p++;}else if(x[p]>0){ //right的右侧,全部>0//元素>0, 将元素与right位置元素 互换int t = x[right];x[right] = x[p];x[p] = t;right--; }else{ //元素==0 left与right中间的全为0
// _________________________; //代码填空位置 p++p++;}}}public static void main(String[] args) {int []arr = {25,18,-2,0,16,-5,33,21,0,19,-16,25,-3,0};sort(arr);for(int x: arr) {System.out.print(x + " ");}}}
七、错误票据
A,B组第7题
标题:错误票据某涉密单位下发了某种票据,并要在年终全部收回。
每张票据有唯一的ID号。全年所有票据的ID号是连续的,但ID的开始数码是随机选定的。
因为工作人员疏忽,在录入ID号的时候发生了一处错误,造成了某个ID断号,另外一个ID重号。
你的任务是通过编程,找出断号的ID和重号的ID。
假设断号不可能发生在最大和最小号。
要求程序首先输入一个整数N(N<100)表示后面数据行数。
接着读入N行数据。
每行数据长度不等,是用空格分开的若干个(不大于100个)正整数(不大于100000)
每个整数代表一个ID号。要求程序输出1行,含两个整数m n,用空格分隔。
其中,m表示断号ID,n表示重号ID例如:
用户输入:
2
5 6 8 11 9
10 12 9则程序输出:
7 9
再例如:
用户输入:
6
164 178 108 109 180 155 141 159 104 182 179 118 137 184 115 124 125 129 168 196
172 189 127 107 112 192 103 131 133 169 158
128 102 110 148 139 157 140 195 197
185 152 135 106 123 173 122 136 174 191 145 116 151 143 175 120 161 134 162 190
149 138 142 146 199 126 165 156 153 193 144 166 170 121 171 132 101 194 187 188
113 130 176 154 177 120 117 150 114 183 186 181 100 163 160 167 147 198 111 119则程序输出:
105 120
资源约定:
峰值内存消耗(含虚拟机) < 64M
CPU消耗 < 2000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.6及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。

package provincialGames_04_2013;import java.util.Scanner;
import java.util.ArrayList;
import java.util.Collections;public class A07_错误票据 { //解题思路:枚举public static void main(String[] args) {Scanner sc = new Scanner(System.in);int N = sc.nextInt();sc.nextLine(); //吃掉整数后的换行符ArrayList<Integer> list = new ArrayList<Integer>(); //动态数组 不知道长度for(int i = 0; i < N; i++) {String line = sc.nextLine();String[] split = line.split(" ");for(int j = 0; j < split.length; j++) {list.add(Integer.parseInt(split[j]));}}//System.out.println(list.size());Collections.sort(list);int brokenNumber = 0, repeatedNumber = 0; //断号、重号for(int i = 1 ; i < list.size(); i++) {if(list.get(i) - list.get(i-1) == 2) {brokenNumber = list.get(i) - 1;}if(list.get(i).equals(list.get(i-1))) { //或list.get(i) - list.get(i-1) == 0,用==得50分 注意此处有坑,不能用==repeatedNumber = list.get(i);}}System.out.println(brokenNumber + " " + repeatedNumber); }}
注意:直接粘贴数据 会报错 :数据转换错误
Exception in thread "main" java.lang.NumberFormatException: For input string: "9 "
at java.lang.NumberFormatException.forInputString(NumberFormatException.java:65)
at java.lang.Integer.parseInt(Integer.java:580)
at java.lang.Integer.parseInt(Integer.java:615)
at provincialGames_04_2013.A07_错误票据.main(A07_错误票据.java:19)
八、幸运数
标题:幸运数
幸运数是波兰数学家乌拉姆命名的。它采用与生成素数类似的“筛法”生成。
首先从1开始写出自然数1,2,3,4,5,6,....
1 就是第一个幸运数。
我们从2这个数开始。把所有序号能被2整除的项删除,变为:1 _ 3 _ 5 _ 7 _ 9 ....
把它们缩紧,重新记序,为:
1 3 5 7 9 .... 。这时,3为第2个幸运数,然后把所有能被3整除的序号位置的数删去。
注意,是序号位置,不是那个数本身能否被3整除!! 删除的应该是5,11, 17, ...此时7为第3个幸运数,然后再删去序号位置能被7整除的(19,39,...)
最后剩下的序列类似:
1, 3, 7, 9, 13, 15, 21, 25, 31, 33, 37, 43, 49, 51, 63, 67, 69, 73, 75, 79, ...
本题要求:
输入两个正整数m n, 用空格分开 (m < n < 1000*1000)
程序输出 位于m和n之间的幸运数的个数(不包含m和n)。例如:
用户输入:
1 20
程序输出:
5例如:
用户输入:
30 69
程序输出:
8资源约定:
峰值内存消耗(含虚拟机) < 64M
CPU消耗 < 2000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.6及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。

package provincialGames_04_2013;import java.util.Scanner;public class A08_幸运数 {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int m = sc.nextInt();int n = sc.nextInt();int[] a = new int[n]; //存储数据的数组for (int i = 0; i < n; i++) {a[i] = 2 * i + 1;}//已经把2的倍数(位置)删除了int l = 1;//幸运数的下标,a[l]是幸运数while (true) {int p = l + 1;//数字向前挪动的坑位for (int i = l + 1; i < n; i++) {if ((i + 1) % a[l] == 0) {} else {a[p] = a[i];p++;}// if (a[i]>n)break;//更正:此处应该是下方的代码if (a[p] > n) { //算法优化处理break; //当a[i] > n, break; 只要n之前的数据}}
// for (int i = 0; i < n; i++) {
// System.out.print(a[i] + " ");
// }
// System.out.println();l++;if(a[l] >= n) {break;}}int ans = 0;for (int i = 0; i < n; i++) {if (a[i] >= n) {break;}if (a[i] > m) {ans++;}}System.out.println(ans);}}
挪一轮:
int l = 1; // 幸运数的下标,a[l]是幸运数
int p = l + 1; // 数字向前挪动的坑位
for (int i = l + 1; i < n; i++) {
if ((i + 1) % a[l] == 0) {
} else {
a[p] = a[i];
p++;
}
}
九、带分数
B组第9题
标题:带分数
100 可以表示为带分数的形式:100 = 3 + 69258 / 714
还可以表示为:100 = 82 + 3546 / 197
注意特征:带分数中,数字1~9分别出现且只出现一次(不包含0)。
类似这样的带分数,100 有 11 种表示法。
题目要求:
从标准输入读入一个正整数N (N<1000*1000)
程序输出该数字用数码1~9不重复不遗漏地组成带分数表示的全部种数。
注意:不要求输出每个表示,只统计有多少表示法!
例如:
用户输入:
100
程序输出:
11再例如:
用户输入:
105
程序输出:
6
资源约定:
峰值内存消耗(含虚拟机) < 64M
CPU消耗 < 3000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.6及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。

package provincialGames_04_2013;import java.util.Scanner;
//1-9 分別出现一次, 求带分数表示种数public class A09_带分数 {static int ans; //全局变量private static int N;public static void main(String[] args) {Scanner sc = new Scanner(System.in);N = sc.nextInt();int[] arr = {1, 2, 3, 4, 5, 6, 7, 8, 9};// int[] arr = {1, 2, 3};f(arr, 0); //全排列函数System.out.println(ans);}//确认某一个排列的第k位private static void f(int[] arr, int k) {if (k == 9) { //全部确认check(arr);// print(arr);return;}//选定第k位,for (int i = k; i < arr.length; i++) {//将第i位和第k位交换int t = arr[i];arr[i] = arr[k];arr[k] = t;// 移交下一层 确认第k+1位f(arr, k + 1);//回溯(换回来) 不影响以后的取值//每一次计算, 都用初始值t = arr[i];arr[i] = arr[k];arr[k] = t;}}// private static void print(int[] arr) {
// for (int i = 0; i < arr.length; i++) {
// System.out.print(arr[i]);
// }
// System.out.println();
// }//枚举加号和除号的位置private static void check(int[] arr) {//+前的字符数最多是7for (int i = 1; i <= 7; i++) {int num1 = toInt(arr, 0, i); //+前面的一段整数if (num1 >= N) continue; //如果此时+号前的数值已经超过了N,没必要验算了// /前面的字符数for (int j = 1; j <= 8 - i; j++) {int num2 = toInt(arr, i, j);int num3 = toInt(arr, i + j, 9 - i - j);if (num2 % num3 == 0 && num1 + num2 / num3 == N) {ans++;}}}}//pos: 开始计算的位置; len:计算的长度(计算len次) 计算区间: [pos, pos + len -1]private static int toInt(int[] arr, int pos, int len) {int t = 1;int ans = 0;for (int i = pos + len - 1; i >= pos; i--) {ans += arr[i] * t;t *= 10;}return ans;}}
int num1 = toInt(arr, 0, i); // "+"前面的一段整数
int num2 = toInt(arr, i, j); // "+"与"/"之间的整数
int num3 = toInt(arr, i + j, 9 - i - j); // "/"后面的整数100 = 3 + 69258 / 714
int num1 = toInt(arr, 0, 1);
int num2 = toInt(arr, 1, 5);
int num3 = toInt(arr, 1 + 5, 9 - 1 - 5);100 = 82 + 3546 / 197
int num1 = toInt(arr, 0, 2);
int num2 = toInt(arr, 2, 4);
int num3 = toInt(arr, 2 + 4, 9 - 2 - 4);
全排列模板——整数数组
package provincialGames_04_2013;public class A09_全排列 {public static void main(String[] args) {int arr1[] = {1, 2, 3, 4, 5, 6, 7, 8, 9};int arr2[] = {1, 2, 3};f(arr1, 0);}//确认某一个排列的第k位private static void f(int[] arr, int k) {if (k == arr.length) //全部确认{for(int x: arr) {System.out.print(x);}System.out.println();return;}//选定第k位,for (int i = k; i < arr.length; i++) {//将第i位和第k位交换int t = arr[i];arr[i] = arr[k];arr[k] = t;// 移交下一层去确认k+1位f(arr, k + 1);//回溯(换回来)t = arr[i];arr[i] = arr[k];arr[k] = t;}}
}
十、连号区间数
标题:连号区间数(同C语言B组第10题)
小明这些天一直在思考这样一个奇怪而有趣的问题:
在1~N的某个全排列中有多少个连号区间呢?这里所说的连号区间的定义是:
如果区间[L, R] 里的所有元素(即此排列的第L个到第R个元素)递增排序后能得到一个长度为R-L+1的“连续”数列,则称这个区间连号区间。
当N很小的时候,小明可以很快地算出答案,但是当N变大的时候,问题就不是那么简单了,现在小明需要你的帮助。
输入格式:
第一行是一个正整数N (1 <= N <= 50000), 表示全排列的规模。
第二行是N个不同的数字Pi(1 <= Pi <= N), 表示这N个数字的某一全排列。输出格式:
输出一个整数,表示不同连号区间的数目。示例:
用户输入:
4
3 2 4 1程序应输出:
7用户输入:
5
3 4 2 5 1程序应输出:
9解释:
第一个用例中,有7个连号区间分别是:[1,1], [1,2], [1,3], [1,4], [2,2], [3,3], [4,4]
第二个用例中,有9个连号区间分别是:[1,1], [1,2], [1,3], [1,4], [1,5], [2,2], [3,3], [4,4], [5,5]
资源约定:
峰值内存消耗(含虚拟机) < 64M
CPU消耗 < 5000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.6及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。

package provincialGames_04_2013;import java.util.Scanner;public class A10_连号区间数 { //穷举、遍历、扫描public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt();int[] arr = new int[n + 1];for (int i = 1; i <= n ; i++) {arr[i] = sc.nextInt();}int ans = 0;for (int i = 1; i <=n ; i++) {int max = arr[i];int min = arr[i];for (int j = i; j <= n ; j++) { // ]的位置if (arr[j] > max) {max = arr[j];}if (arr[j] < min) {min = arr[j];}// j 只能 >= iif (i == j){// System.out.printf("[%d,%d]\n",i,j);ans++;} else{ //i<j,判断[i,j]是连号区间if (max - min == j - i){// System.out.printf("[%d,%d]\n",i,j);ans++;}}}}System.out.println(ans);}}
小结
01 世纪末的星期 枚举每个世纪末,判断是否星期天 Calendar
02 马虎的算式 枚举每个位上的数字,组合判断
03 振兴中华 找重复中的变化,找边界
**04 黄金连分数 1.识别问题等价于斐波那契的n项和n+1项的比值,2.n要多少才够,3.怎么处理很大的数和精度要求很高的浮点数05 有理数类 面向对象+分数加法(通分与约分)
06 三部排序 快速排序(三指针区间法)变体;极限思维(考虑全部是0)07 错误票据 输入比较特殊,排序,迭代(获取断号和重号),输出
08 幸运数 模拟筛选过程,枚举计数
09 带分数 1-9用递归做全排列,对每一个排列,都枚举+和/的位置,然后进行检查
10 连号区间数 枚举所有区间,检查这个区间里面的数排序后是否连号



