ADPRL - 近似动态规划和强化学习 - Note 5 - Banach Fixed Point Theorem in Dynamic Programming

5. Banach Fixed Point Theorem in Dynamic Programming

如上两节所示，VI算法和PI算法都拥有各自的优势和劣势。具体来说，VI算法是一种简单的迭代算法，但它在总成本函数空间的收敛性方面可能是低效的。虽然PI算法在探索策略空间的有限性和在策略空间中达到更好的收敛性方面有一个很好的特性，但它仍然会受到精确策略评估的瓶颈影响。尽管OPI算法自然地连接了这两种算法，但它的性能是由有限策略评估的数量选择决定的。在本节中，我们旨在通过探索巴拿赫固定点定理的属性来缓解这种限制，并仍然保留简单和快速收敛的有希望的属性。

5.1 巴拿赫不动点定理定理 （Banach fixed point theorem）

首先，为了讨论的完整性，我们回顾一下最近提出的、证明压缩原理的另一种方法[19]。

定义 5.1 度量空间定义

度量空间是一有序对$(\mathcal{X},d)$
$(\mathcal{X},d)$ 其中$\mathcal{X}$是一个集合, $d$ 是一个在 $\mathcal{X}$的度量, 即, 一个函数$d:\mathcal{X}\times \mathcal{X}\to \mathbb{R}$, 对于所有$x,y,z\in \mathcal{X}$, 以下关系成立:

1. $d(x,y)=0?x=y$ 不可分者同一性原理 (identity of indiscernibles),

2. $d(x,y)=d(y,x)$ 对称性 (symmetry)

3. $d(x,z)\le d(x,y)+d(y,z)$ 三角不等式 (triangle inequality).

定义 5.2 压缩映射

令$(\mathcal{X},d)$为一度量空间，映射关系 $\mathrm{T}:\mathcal{X}\to \mathcal{X}$被称为在$\mathcal{X}$上的压缩映射，如果存在$\gamma \in [0,1)$， 使得

$$d(\mathrm{T}(x),\mathrm{T}(y))\le \gamma d(x,y),\text{ for all }x,y\in \mathcal{X}\text{\hspace{1em}(5.1)}$$

Lemma 5.1 基本压缩不等式 (Fundamental contraction inequality)

如果$\mathrm{T}:\mathcal{X}\to \mathcal{X}$ 是一个压缩常数为$\gamma$的压缩映射，那么对于在 $\mathcal{X}$ 的任意$x,y$
$$d(x,y)\le \frac{1}{1?\gamma }(d(x,\mathrm{T}(x))+d(y,\mathrm{T}(y)))\text{\hspace{1em}(5.2)}$$

---

Proof

根据三角不等式和$\mathrm{T}$是一个压缩映射的事实，我们有
$$\begin{array}{rl}d(x,y)& \le d(x,\mathrm{T}(x))+d(\mathrm{T}(x),\mathrm{T}(y))+d(\mathrm{T}(y),y)\\ & \le d(x,\mathrm{T}(x))+\gamma d(x,y)+d(\mathrm{T}(y),y)\end{array}\text{\hspace{1em}(5.3)}$$

即证。

---

Corollary 5.1 压缩映射的固定点

一个压缩映射$\mathrm{T}$最多有一个固定点。

---

Proof

让我们假设压缩映射 $T$有一个以上的固定点，例如$x$和$y$，$d(x,y)=0.$ 根据$\mathrm{T}$的固定点定义，我们得到$d(x,\mathrm{T}(x))=0$ 和$d(y,\mathrm{T}(y))=0$。根据Lemma 5.1，我们有$d(x,y)=0.$ 通过矛盾法，即证。

---

Proposition 5.1 柯西序列

如果$\mathrm{T}$是一个压缩，那么对于任何$x\in \mathcal{X}$，${\mathrm{T}}^k(x)$下$x$的迭代序列$\mathrm{T}$是一个柯西序列 (Cauchy sequence)。

---

Proof

让$x_1={\mathrm{T}}^k(x)$ 和$x_2={\mathrm{T}}^l(x).$ 那么，根据基本压缩不等式，我们有
$$\begin{array}{rl}d\left({\mathrm{T}}^k(x),{\mathrm{T}}^l(x)\right)& \le \frac{1}{1?\gamma }\left(d\left({\mathrm{T}}^k(x),{\mathrm{T}}^{k+1}(x)\right)+d\left({\mathrm{T}}^l(x),{\mathrm{T}}^{l+1}(x)\right)\right)\\ & \le \frac{{\gamma }^k+{\gamma }^l}{1?\gamma }(d(x,\mathrm{T}(x))+d(x,\mathrm{T}(x)))\end{array}\text{\hspace{1em}(5.4)}$$

显然，当$k$和$l$趋于无穷大时，$d\left({\mathrm{T}}^k(x),{\mathrm{T}}^l(x)\right)$的距离会归于零。最后，我们准备提出经典的巴拿赫不动点定理(Banach fixed-point theorem)。

---

Theorem 5.1 巴拿赫不动点定理 (The Banach fixed-point theorem)

让$(\mathcal{X},d)$是一个非空的完整度量空间，有一个压缩映射$\mathrm{T}$。那么$\mathrm{T}$就有一个唯一的固定点$x^{?}$。即 $\mathrm{T}\left(x^{?}\right)=x^{?}$。此外，$x^{?}$可以通过迭代来找到。

$$x_{n+1}=\mathrm{T}\left(x_n\right),\text{ with arbitrary }{x}_0\in \mathcal{X}\text{\hspace{1em}(5.5)}$$

也就是说，当$n\to \infty$时，有$x_n\to x^{?}$ 。

---

Proof
直接的，我们有

$$d\left({\mathrm{T}}^k(x),x^{?}\right)\le \frac{{\gamma }^k}{1?\gamma }d(x,\mathrm{T}(x))\text{\hspace{1em}(5.6)}$$

即, $k\to \infty$ 导致${\mathrm{T}}^k(x)$收敛到 $x^{?}$.

5.2 $\lambda$-几何平均贝尔曼算子 ($\lambda$-geometrically averaged Bellman operator)

利用OPI算法的一个可能的方法是将各种OPI算法与不同步骤的策略评估集合起来。具体来说，我们可以根据$\mathrm{E}\mathrm{q}.(4.33)$中定义的$m$步骤贝尔曼算子的集合构建一个几何平均贝尔曼算子。
$$\begin{array}{rl}{\mathrm{T}}_{\pi ,\lambda }^m:{\mathbb{R}}^K\to {\mathbb{R}}^K,J& ?\frac{1}{{\sum }_{i=1}^m{\lambda }^{i?1}}\sum _{i=1}^m{\lambda }^{i?1}{\mathrm{T}}_{\pi }^{i}J\\ & =\frac{1?\lambda }{1?{\lambda }^m}\sum _{i=1}^m{\lambda }^{i?1}{\mathrm{T}}_{\pi }^{i}J\end{array}\text{\hspace{1em}(5.7)}$$

很容易看出，总成本函数$J_{\pi }$是所有$m$步贝尔曼算子的唯一固定点。它的压缩特性在下面的结果中得到了描述。

Proposition 5.2 $m$步的几何平均贝尔曼算子的压缩特性 (Contraction property of $m$-step geometrically averaged Bellman operator)

给定无限范围的MDP{X,U,p,g,γ}M D P\{\mathcal{X}, \mathcal{U}, p, g, \gamma\}MDP{ X,U,p,g,γ}, 令$J,J^{\prime }\in {\mathbb{R}}^K$, $m?$步截断的、几何平均的贝尔曼算子是一个关于无穷范数的压缩映射，即：

$${\Vert {\mathrm{T}}_{\pi ,\lambda }^{m}J?{\mathrm{T}}_{\pi ,\lambda }^m{J}^{\prime }\Vert }_{\infty }\le \frac{\gamma \left(1?{\lambda }^m{\gamma }^m\right)(1?\lambda )}{(1?\lambda \gamma )\left(1?{\lambda }^m\right)}{\Vert J?J^{\prime }\Vert }_{\infty }\text{\hspace{1em}(5.8)}$$

---

Proof

根据无穷范数的三角不等式，可以得出
$$\begin{array}{rl}{\Vert {\mathrm{T}}_{\pi ,\lambda }^{m}J?{\mathrm{T}}_{\pi ,\lambda }^m{J}^{\prime }\Vert }_{\infty }& =\frac{1?\lambda }{1?{\lambda }^m}{\Vert \sum _{i=1}^m{\lambda }^{i?1}\left({\mathrm{T}}_{\pi }^{i}J?{\mathrm{T}}_{\pi }^i{J}^{\prime }\right)\Vert }_{\infty }\\ & \le \frac{1?\lambda }{1?{\lambda }^m}\left(\sum _{i=1}^m{\lambda }^{i?1}{\Vert {\mathrm{T}}_{\pi }^{i}J?{\mathrm{T}}_{\pi }^i{J}^{\prime }\Vert }_{\infty }\right)\\ & \le \frac{1?\lambda }{1?{\lambda }^m}\left(\sum _{i=1}^m{\lambda }^{i?1}{\gamma }^i{\Vert J?J^{\prime }\Vert }_{\infty }\right)\\ & \le \frac{\gamma (1?\lambda )\left(1?{\lambda }^m{\gamma }^m\right)}{(1?\lambda \gamma )\left(1?{\lambda }^m\right)}{\Vert J?J^{\prime }\Vert }_{\infty }\end{array}\text{\hspace{1em}(5.9)}$$

由于压缩系数严格小于1，即证。

---

值得注意的是，当策略评估的数量$m$增加时，几何平均贝尔曼算子${\mathrm{T}}_{\pi ,\lambda }^m$的压缩系数就会下降。换句话说，$m$的总成本越大，相关算法的收敛速度就越快。请注意，当$m$的总成本上升到无穷大时，这样的结构实际上是不现实的。然而，通过使$m$的总成本达到无穷大，很容易得出几何平均的贝尔曼算子为

$${\mathrm{T}}_{\pi ,\lambda }^{\infty }:{\mathbb{R}}^K\to {\mathbb{R}}^K,J?(1?\lambda )\sum _{i=1}^{\infty }{\lambda }^{i?1}{\mathrm{T}}_{\pi }^{i}J\text{\hspace{1em}(5.10)}$$

在我们的Notes中被称为$\lambda$几何平均贝尔曼算子。

Proposition 5.3 $\lambda$几何平均贝尔曼算子的压缩性 (Contraction property of the $\lambda$-geometrically averaged Bellman operator)

给定一个无限范围MDP{X,U,p,g,γ}M D P\{\mathcal{X}, \mathcal{U}, p, g, \gamma\}MDP{ X,U,p,g,γ}，让$J,J^{\prime }\in {\mathbb{R}}^K$，$\lambda$几何平均贝尔曼算子是一个关于无穷范数的压缩映射，即

$${\Vert {\mathrm{T}}_{\pi ,\lambda }^{\infty }J?{\mathrm{T}}_{\pi ,\lambda }^{\infty }{J}^{\prime }\Vert }_{\infty }\le \frac{\gamma (1?\lambda )}{1?\lambda \gamma }{\Vert J?J^{\prime }\Vert }_{\infty }\text{\hspace{1em}(5.11)}$$

---

Proof
这个结果来自于如命题5.2(eq. )中的将$m$推导到无穷大。

---

显然，$\lambda$几何平均贝尔曼算子只有理论上的意义，没有实际用途。在下文中，我们研究了一个精心设计的贝尔曼算子，它最初是受$\lambda$几何平均贝尔曼算子启发。它与RL背景下的 资格迹（eligibility trace） 概念的联系将在后面的章节中讨论。

5.3 $\lambda$-策略迭代算法 （$\lambda$-Policy Iteration Algorithm）

让$J^{\prime }\in {\mathbb{R}}^K$成为总成本函数$J_{\pi }\in {\mathbb{R}}^K$的一个估计。我们定义以下映射
$${\mathrm{T}}_{\pi ,J^{\prime }}^{(\lambda )}:{\mathbb{R}}^K\to {\mathbb{R}}^K,J?(1?\lambda ){\mathrm{T}}_{\pi }{J}^{\prime }+\lambda {\mathrm{T}}_{\pi }J\text{\hspace{1em}(5.12)}$$

我们称其为称为$\lambda$-级联贝尔曼算子（$\lambda$-cascaded Bellman operator）。很容易看出，对于任何$J_1,J_2\in {\mathbb{R}}^K$中，我们有
$$\begin{array}{rl}{\Vert {\mathrm{T}}_{\pi ,J^{\prime }}^{(\lambda )}{J}_1?{\mathrm{T}}_{\pi ,J^{\prime }}^{(\lambda )}{J}_2\Vert }_{\infty }& \le \lambda {\Vert {\mathrm{T}}_{\pi }{J}_1?{\mathrm{T}}_{\pi }{J}_2\Vert }_{\infty }\\ & \le \lambda \gamma {\Vert J_1?J_2\Vert }_{\infty }\end{array}\text{\hspace{1em}(5.13)}$$

显然，$\lambda$-级联贝尔曼算子是一个压缩，其模为$\lambda \gamma$，相对于无穷范数。也就是说，它有一个唯一的固定点。当$\lambda =0$时，${\mathrm{T}}_{\pi ,J^{\prime }}^{(0)}$的固定点是${\mathrm{T}}_{\pi }{J}^{\prime }$，这基本上是贝尔曼算子${\mathrm{T}}_{\pi }$对估计值$J^{\prime }$的一步应用。 当$\lambda =1$时，${\mathrm{T}}_{\pi ,J^{\prime }}^{(1)}$的固定点满足以下等式
$$J={\mathrm{T}}_{\pi }J\text{\hspace{1em}(5.14)}$$

这确实是策略$\pi$的真实总成本函数，即$J_{\pi }$因此，公式（5.12）中定义的$\lambda$-级联贝尔曼算子$T_{\pi ,J^{\prime }}^{（\lambda ）}$的固定点可以被视为单步贝尔曼算子和无限步贝尔曼算子的凸组合。这样的关系与$\lambda$-贝尔曼算子${\mathrm{T}}_{\pi }^{\infty }$的构造相吻合。

有趣的是，$\lambda$-级联贝尔曼算子的单调性和恒定位移特性也都得到了保留。

Lemma 5.2 $\lambda$-级联的贝尔曼算子的单调性和恒定位移特性 (Monotonicity and constant shift of the $\lambda$-cascaded Bellman operator)

给定一个无限范围MDP{X,U,p,g,γ}M D P\{\mathcal{X}, \mathcal{U}, p, g, \gamma\}MDP{ X,U,p,g,γ}，$\lambda$-级联贝尔曼算子${\mathrm{T}}_{\pi ,J^{\prime }}^{(\lambda )}$同时具有单调性和恒移性。

(1) 对于所有$x\in \mathcal{X}$，让$J_1,J_2\in {\mathbb{R}}^K$ 满足$J_1(x)\le J_2(x)$。那么对于$k=1,2,\dots$，我们有
$${\left({\mathrm{T}}_{\pi ,J^{\prime }}^{(\lambda )}\right)}^k{J}_1(x)\le {\left({\mathrm{T}}_{\pi ,J^{\prime }}^{(\lambda )}\right)}^k{J}_2(x)\text{\hspace{1em}(5.15)}$$

(2) 让$J_1,J_2\in {\mathbb{R}}^K$ 满足$J_2$为$J_1$的常数移位函数的构造，即对于所有$x\in \mathcal{X}$有$J_2(x)=J_1(x)+c$。那么对于$k=1,2,\dots$，我们有

$${\left({\mathrm{T}}_{\pi ,J^{\prime }}^{(\lambda )}\right)}^k{J}_2(x)={\left({\mathrm{T}}_{\pi ,J^{\prime }}^{(\lambda )}\right)}^k{J}_1(x)+{\lambda }^k{\gamma }^{k}c\text{\hspace{1em}(5.16)}$$

---

Proof
回忆定义 ${\mathrm{T}}_{\pi ,J^{\prime }}^{(\lambda )}$, 我们有

$$\begin{array}{rl}{\mathrm{T}}_{\pi ,J^{\prime }}^{(\lambda )}{J}_1& =(1?\lambda ){\mathrm{T}}_{\pi }{J}^{\prime }+\lambda {\mathrm{T}}_{\pi }{J}_1\\ & \le (1?\lambda ){\mathrm{T}}_{\pi }{J}^{\prime }+\lambda {\mathrm{T}}_{\pi }{J}_2\\ & ={\mathrm{T}}_{\pi ,J^{\prime }}^{(\lambda )}{J}_2\end{array}\text{\hspace{1em}(5.17)}$$

其中不等式是由于标准贝尔曼算子 ${\mathrm{T}}_{\pi }$的单调性，以及
$$\begin{array}{rl}{\mathrm{T}}_{\pi ,J^{\prime }}^{(\lambda )}{J}_2& =(1?\lambda ){\mathrm{T}}_{\pi }{J}^{\prime }+\lambda {\mathrm{T}}_{\pi }\left(J_1+c1\right)\\ & =(1?\lambda ){\mathrm{T}}_{\pi }{J}^{\prime }+\lambda {\mathrm{T}}_{\pi }{J}_1+\lambda \gamma c1\\ & ={\mathrm{T}}_{\pi ,J^{\prime }}^{(\lambda )}{J}_1+\lambda \gamma c1\end{array}\text{\hspace{1em}(5.18)}$$

这个结果简单的从一个归纳论证中得出。

---

Proposition 5.4 $\lambda$-级联的贝尔曼算子的压缩特性 (Contraction property of the $\lambda$-cascaded Bellman operator)

给定一个无限范围MDP{X,U,p,g,γ}M D P\{\mathcal{X}, \mathcal{U}, p, g, \gamma\}MDP{ X,U,p,g,γ}，以及两个总成本函数估计值$J_1,J_2\in {\mathbb{R}}^K$是有边界的。$\lambda$-级联贝尔曼算子是一个关于无穷范数模为$\lambda \gamma$的压缩，即，

$${\Vert {\mathrm{T}}_{\pi ,J^{\prime }}^{(\lambda )}{J}_1?{\mathrm{T}}_{\pi ,J^{\prime }}^{(\lambda )}{J}_2\Vert }_{\infty }\le \lambda \gamma {\Vert J_1?J_2\Vert }_{\infty }\text{\hspace{1em}(5.19)}$$

此外，$\lambda$几何平均贝尔曼算子在$J^{\prime }$的一步评估是${\mathrm{T}}_{\pi ,J^{\prime }}^{(\lambda )}$的唯一固定点，即,
$${\mathrm{T}}_{\pi ,J^{\prime }}^{(\lambda )}\left({\mathrm{T}}_{\pi ,\lambda }^{\infty }{J}^{\prime }\right)={\mathrm{T}}_{\pi ,\lambda }^{\infty }{J}^{\prime }\text{\hspace{1em}(5.20)}$$

---

Proof
直接的有

$$\begin{array}{rl}{\Vert {\mathrm{T}}_{\pi ,J^{\prime }}^{(\lambda )}{J}_1?{\mathrm{T}}_{\pi ,J^{\prime }}^{(\lambda )}{J}_2\Vert }_{\infty }& \le {\Vert \lambda {\mathrm{T}}_{\pi }{J}_1?\lambda {\mathrm{T}}_{\pi }{J}_2\Vert }_{\infty }\\ & \le \lambda \gamma {\Vert J_1?J_2\Vert }_{\infty }\end{array}\text{\hspace{1em}(5.21)}$$

其中简单地遵循贝尔曼算子的特性。将结果${\mathrm{T}}_{\pi ,\lambda }^{\infty }{J}^{\prime }$ 代入到${\mathrm{T}}_{\pi ,J^{\prime }}$ 得到，

$$\begin{array}{rl}{\mathrm{T}}_{\pi ,J^{\prime }}^{(\lambda )}\left({\mathrm{T}}_{\pi ,\lambda }^{\infty }{J}^{\prime }\right)& ={\mathrm{T}}_{\pi ,J^{\prime }}^{(\lambda )}\left((1?\lambda )\sum _{k=1}^{\infty }{\lambda }^{k?1}{\mathrm{T}}_{\pi }^k{J}^{\prime }\right)\\ & =(1?\lambda ){\mathrm{T}}_{\pi }{J}^{\prime }+\lambda {\mathrm{T}}_{\pi }\left((1?\lambda )\sum _{k=1}^{\infty }{\lambda }^{k?1}{\mathrm{T}}_{\pi }^k{J}^{\prime }\right)\\ & =(1?\lambda ){\mathrm{T}}_{\pi }{J}^{\prime }+(1?\lambda )\sum _{k=2}^{\infty }{\lambda }^{k?1}{\mathrm{T}}_{\pi }^k{J}^{\prime }\\ & =(1?\lambda )\sum _{k=1}^{\infty }{\lambda }^{k?1}{\mathrm{T}}_{\pi }^k{J}^{\prime }\end{array}\text{\hspace{1em}(5.22)}$$

即证。

---

显然，$\lambda$几何平均贝尔曼算子${\mathrm{T}}_{\pi ,\lambda }^{\infty }$的评估可以通过找到$\lambda$-级联贝尔曼算子${\mathrm{T}}_{\pi ,J^{\prime }}^{(\lambda )}$的固定点直接计算，即
$$J=(1?\lambda ){\mathrm{T}}_{\pi }{J}^{\prime }+\lambda {\mathrm{T}}_{\pi }J\text{\hspace{1em}(5.23)}$$

在MDP的背景下，我们可以利用贝尔曼算子的紧凑表述的便利，如公式$(4.25)$，这导致了固定点的闭式表达为
$$J={\left(I_K?\gamma \lambda P_{\pi }\right)}^{?1}\left(G_{\pi }+\gamma (1?\lambda )P_{\pi }{J}^{\prime }\right)\text{\hspace{1em}(5.24)}$$

通过采取与第4.4节中开发最优策略迭代相同的方法，我们构造了一个最优$\lambda$策略迭代算法（Algorithm 4）。与证明Proposition 4.7的策略相同，可以得出以下关于最优$\lambda$-PI算法的收敛性的结果

Proposition 5.5 最优$\lambda$-PI算法的收敛性 (Convergence of Optimistic $\lambda$-PI Algorithm)

给定一个无限范围MDP {X,U,p,g,γ}\{\mathcal{X}, \mathcal{U}, p, g, \gamma\}{ X,U,p,g,γ}，让{Jk}\left\{J_{k}\right\}{ Jk?}和{πk}\left\{\pi_{k}\right\}{ πk?}是由最优$\lambda$-PI算法生成的序列。然后$J_k$收敛到$J^{?}$。此外，对于所有指数$k$大于某个指数$\kappa$，${\pi }_k$对于所有$k>\kappa$来说是最优的。

$${\Vert J_{k+1}?J^{?}\Vert }_{\infty }\le \left(\frac{\gamma (1?\lambda )\left(1?{\lambda }^m{\gamma }^m\right)}{1?\lambda \gamma }+{\lambda }^m{\gamma }^m\right){\Vert J_k?J^{?}\Vert }_{\infty }\text{\hspace{1em}(5.25)}$$

---

Proof

与简单OPI算法的证明类似，我们假设${\mathrm{T}}_{\mathfrak{g}}{J}_0\le J_0$。应用策略改进，即${\mathrm{T}}_{{\pi }_0}{J}_0={\mathrm{T}}_{\mathfrak{g}}{J}_0$，意味着

$${\mathrm{T}}_{{\pi }_0,J_0}^{(\lambda )}{J}_0={\mathrm{T}}_{{\pi }_0}{J}_0={\mathrm{T}}_{\mathfrak{g}}{J}_0\le J_0\text{\hspace{1em}(5.26)}$$

让我们假设${\mathrm{T}}_{{\pi }_k}{J}_k\le J_k$。根据公式（5.12）中$\lambda$-级联贝尔曼算子的定义，我们有
$${\mathrm{T}}_{{\pi }_k,J_k}^{(\lambda )}{J}_k={\mathrm{T}}_{{\pi }_k}{J}_k={\mathrm{T}}_{\mathfrak{g}}{J}_k\le J_k\text{\hspace{1em}(5.27)}$$

然后结构 $J_{k+1}={\left({\mathrm{T}}_{{\pi }_k,J_k}^{(\lambda )}\right)}^{m_k}{J}_k$ 意味着 $J_{k+1}\le J_k$。因此，我们有

$$\begin{array}{rl}{\mathrm{T}}_{{\pi }_{k+1}}{J}_{k+1}& ={\mathrm{T}}_{\mathfrak{g}}{J}_{k+1}\\ & \le {\mathrm{T}}_{{\pi }_k{J}_{k+1}}\\ & =(1?\lambda ){\mathrm{T}}_{{\pi }_k}{J}_{k+1}+\lambda {\mathrm{T}}_{{\pi }_k}{J}_{k+1}\\ & \le (1?\lambda ){\mathrm{T}}_{{\pi }_k}{J}_k+\lambda {\mathrm{T}}_{{\pi }_k}{J}_{k+1}\\ & ={\mathrm{T}}_{{\pi }_k,J_k}^{(\lambda )}{J}_{k+1}\\ & ={\mathrm{T}}_{{\pi }_k,J_k}^{(\lambda )}?{\left({\mathrm{T}}_{{\pi }_k,J_k}^{(\lambda )}\right)}^{m_k}{J}_k\\ & \le J_{k+1},\end{array}\text{\hspace{1em}(5.28)}$$

其中最后一个不等式由$\lambda$-级联贝尔曼算子的单调性得出。简而言之，我们只需证明不等式

$${\mathrm{T}}_{{\pi }_k,J_k}^{(\lambda )}{J}_k={\mathrm{T}}_{{\pi }_k}{J}_k={\mathrm{T}}_{\mathfrak{g}}{J}_k\le J_k\text{\hspace{1em}(5.29)}$$

对于由最优$\lambda$策略迭代算法产生的所有$J_k$序列都成立。最后，对于任何$k$，我们有
$$\begin{array}{rl}{J}_{k+1}& ={\left({\mathrm{T}}_{{\pi }_k,J_k}^{(\lambda )}\right)}^{m_k}{J}_k\\ & \le {\mathrm{T}}_{{\pi }_k}{J}_k\\ & ={\mathrm{T}}_{\mathfrak{g}}{J}_k\end{array}\text{\hspace{1em}(5.30)}$$

作为结果有，
$$J^{?}\le J_k\le {\mathrm{T}}_{\mathfrak{g}}^k{J}_0\text{\hspace{1em}(5.31)}$$

$k\to \infty$导致的结果是$J_k$在极限时收敛于$J^{?}$。 没有假设 ${\mathrm{T}}_{\mathfrak{g}}{J}_0\le J_0$的结果与证明命题4.7的思路相同。

对于所有步骤我们假设$m_k=m$。由于$J_k\to J^{?}$，因此，对于所有$k$大于某个指数$\kappa$，使${\pi }_k$为最优策略，即${\mathrm{T}}_{{\pi }_k}={\mathrm{T}}_{\mathfrak{g}}$。 因此，我们有

$$\begin{array}{rl}{\Vert J_{k+1}?J^{?}\Vert }_{\infty }& ={\Vert {\left({\mathrm{T}}_{{\pi }_k,J_k}^{(\lambda )}\right)}^m{J}_k?J^{?}\Vert }_{\infty }\\ & ={\Vert (1?\lambda )\sum _{i=1}^m{\lambda }^{i?1}{\mathrm{T}}_{{\pi }_k}^i{J}_k+{\lambda }^m{\mathrm{T}}_{{\pi }_k}^m{J}_k?{\mathrm{T}}_{{\pi }_k}{J}^{?}\Vert }_{\infty }\\ & \le \left(\frac{\gamma (1?\lambda )\left(1?{\lambda }^m{\gamma }^m\right)}{1?\lambda \gamma }+{\lambda }^m{\gamma }^m\right){\Vert J_k?J^{?}\Vert }_{\infty }\end{array}\text{\hspace{1em}(5.32)}$$

其中，不等式由无穷范数的三角不等式得出。结果即证。

---

Remark 5.1

当$m=1$时，该结果与基本VI算法的结果相吻合。当$m\to \infty$，对于所有$k$大于某个指数$\kappa$，使得${\pi }_k$是一个最优策略时，总成本函数的收敛特点为
$${\Vert J_{k+1}?J^{?}\Vert }_{\infty }\le \frac{\gamma (1?\lambda )}{1?\lambda \gamma }{\Vert J_k?J^{?}\Vert }_{\infty }\text{\hspace{1em}(5.33)}$$

这与命题5.3中的$\lambda$-几何平均贝尔曼算子的结果一致。

5.4 实例

Question 1: Optimistic $\lambda$ -Policy Iteration: E-Bus, extended

Consider a group of electric buses running round trips 24 hours a day. The task is to identify optimal operating actions at different battery states. The battery’s endurance and charging speed gradually decrease with the increase of battery life. Hence, for different buses, they have different transition probabilities between battery states. The following figure illustrates the state transitions between different states.

• Five states: $H$ - high battery, $E$ - empty battery, $L_1,L_2,L_3$ : three different low level battery statuses
• Two actions: $S$- continue to serve, C - charge
• Numbers on the edges refer to transition probabilities. $p_1=0.4,p_2=0.6$
• Discount factor $\gamma =0.9$ .

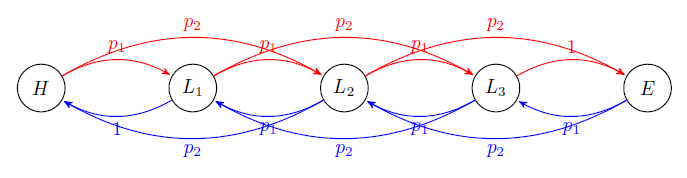
We choose the number of unserviced passengers as the local costs:

• In the high battery state, if it keeps the service, the unserviced passenger number is 0 .
• In all the low battery stats, if it keeps the service, the unserviced passenger number is 2 .
• In all the low battery state and empty battery, if it charges the battery, the unserviced passenger number is 5 .

Task 1

Implement one sweep of $\lambda$ -Policy Iteration Algorithm. Let us initialize total cost $J_0=0$ and $\lambda =0.8$ .
(i) Generate a GIP ${\pi }_0$ from $J_0$ , and define its Bellman operator ${\mathrm{T}}_{{\pi }_0}$ ;
(ii) Iterate the Bellman operator ${\mathrm{T}}_{{\pi }_0}$ on $J_0$ till reaching the stopping criterion as ${\Vert J_{i+1}?J_i\Vert }_{\infty }<10^{?20}$ , where $J_i$ 's are evaluations of ${\mathrm{T}}_{{\pi }_0}$
(iii) Iterate the \lambda -cascaded Bellman operator $T_{{\pi }_0,J_0}^{(\lambda )}$ on $J_0$ till reaching the same stopping criterion as in (ii);
(iv) Compare the results by task (ii) and (iii), as well as the number of iterations required till stopping.

import numpy as np
import matplotlib.pyplot as plt# transition probability
p1 = 0.4
p2 = 0.6# initial cost function
jh = jl1 = jl2 = jl3 = je = 0# cost of each state-action pair
ghs = 0
gl1s = gl2s = gl3s = 2
gec = gl3c = gl2c = gl1c = 5lmbd = 0.6
gamma = 0.9  # discount factordef T_pi(J_k, ul1, ul2, ul3):"""J_k: numpy array, total cost of five statesul1, ul2, ul3: str, 'S' or 'C'return: numpy array, updated total cost of five states"""jh, jl1, jl2, jl3, je = float(J_k[0]), float(J_k[1]), float(J_k[2]), float(J_k[3]), float(J_k[4])jh_ = p1 * (ghs + gamma * jl1) + p2 * (ghs + gamma * jl2)  # Sif ul1 == 'S':jl1_ = p1 * (gl1s + gamma * jl2) + p2 * (gl1s + gamma * jl3)elif ul1 == 'C':jl1_ = gl1c + gamma * jhif ul2 == 'S':jl2_ = p1 * (gl2s + gamma * jl3) + p2 * (gl2s + gamma * je)elif ul2 == 'C':jl2_ = p1 * (gl2c + gamma * jl1) + p2 * (gl2c + gamma * jh)if ul3 == 'S':jl3_ = gl3s + gamma * jeelif ul3 == 'C':jl3_ = p1 * (gl3c + gamma * jl2) + p2 * (gl3c + gamma * jl1)je_ = p1 * (gec + gamma * jl3) + p2 * (gec + gamma * jl2)  # Creturn np.array([jh_, jl1_, jl2_, jl3_, je_])# Q1: Generate GIP and its Bellman operator T_pi0
jl1_all = [p1 * (gl1s + gamma * jl2) + p2 * (gl1s + gamma * jl3), gl1c + gamma * jh]
ul1 = jl1_all.index(min(jl1_all))jl2_all = [p1 * (gl2s + gamma * jl3) + p2 * (gl2s + gamma * je),p1 * (gl2c + gamma * jl1) + p2 * (gl2c + gamma * jh)]
ul2 = jl2_all.index(min(jl2_all))jl3_all = [gl3s + gamma * je,p1 * (gl3c + gamma * jl2) + p2 * (gl3c + gamma * jl1)]
ul3 = jl3_all.index(min(jl3_all))Actions = ['S', 'C']
print('Q1:\tThe GIPs of L1, L2, L3 are {}, {}, {}'.format(Actions[ul1], Actions[ul2], Actions[ul3]))J_i = [0., 0., 0., 0., 0.]
T_pi0 = T_pi(J_i, Actions[ul1], Actions[ul2], Actions[ul3])
print('\t and its Bellman operator are {}'.format(T_pi0))# Q2 : the number of iterations of Bellman operator
Threshold = 1
i = 0
J_i_data = []
while Threshold > 1e-2:J_i_ = T_pi(J_i, Actions[ul1], Actions[ul2], Actions[ul3])Threshold = max(abs(J_i_ - J_i))J_i_data.append(J_i)J_i = J_i_i += 1print('\nQ2: After {} iterations the cost function J_i are {}'.format(i, J_i))# Q3： the number of iterations of lambda-cascade Bellman operator
Threshold = 1
k = 0
J_k = [0., 0., 0., 0., 0.]
J_0 = [0., 0., 0., 0., 0.]
J_k_data = []
while Threshold > 1e-2:J_k_ = (1 - lmbd) * T_pi(J_0, Actions[ul1], Actions[ul2], Actions[ul3]) \+ lmbd * (T_pi(J_k, Actions[ul1], Actions[ul2], Actions[ul3]))Threshold = max(abs(J_k_ - J_k))J_k_data.append(J_k)J_k = J_k_k += 1print('\nQ3: After {} iterations the cost function J_k are {}'.format(k, J_k))# Q4: compare the results and plot the results
J_i_error = np.max(np.array(abs(J_i_data - J_i)), axis=1)
J_k_error = np.max(np.array(abs(J_k_data - J_k)), axis=1)
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.set_xlabel('Iteration i')
ax.set_ylabel('$||J - J*||_{\infty}$')
ax.plot(J_i_error, marker='*', label='$PE$')
ax.plot(J_k_error, marker='.', label='$\lambda \ - \ PE$')
ax.legend()
ax.set_title('Threshlod = 0.01')
plt.show()

Th outputs are:

Q1:	The GIPs of L1, L2, L3 are S, S, Sand its Bellman operator are [0. 2. 2. 2. 5.]Q2: After 57 iterations the cost function J_i are [28.71067246 31.33441578 32.29354488 32.80920569 34.24159683]Q3: After 11 iterations the cost function J_k are [3.15423695 5.43385663 6.12451136 6.52698135 8.39038175]

Task 2

Implement and run the \lambda -Policy Iteration Algorithm till convergence to generate an optimal policy. Let us set the number of optimistic $\lambda$ -Policy evaluation step $m_k=5$ .

# Task 2 : generate the optimal policy
print('\n-------The optimal policy---------\n')
J_k = np.array([0., 0., 0., 0., 0.])
for k in range(0, 5):# Policy Inprovementjh, jl1, jl2, jl3, je = J_kul1 = np.argmin([p1 * (gl1s + gamma * jl2) + p2 * (gl1s + gamma * jl3), gl1c + gamma * jh])ul2 = np.argmin([p1 * (gl2s + gamma * jl3) + p2 * (gl2s + gamma * je),p1 * (gl2c + gamma * jl1) + p2 * (gl2c + gamma * jh)])ul3 = np.argmin([gl3s + gamma * je,p1 * (gl3c + gamma * jl2) + p2 * (gl3c + gamma * jl1)])# Policy Evaluationfor m in range(5):J_k_ = (1 - lmbd) * T_pi(J_k, Actions[ul1], Actions[ul2], Actions[ul3]) \+ lmbd * (T_pi(J_k, Actions[ul1], Actions[ul2], Actions[ul3]))J_k = J_k_print('In {}-th step the optimal policy are in L1 is {}, in L2 is {}, ''in L3 is {}'.format(k, Actions[ul1], Actions[ul2], Actions[ul3]))

the outputs are

-------The optimal policy---------In 0-th step the optimal policy are in L1 is S, in L2 is S, in L3 is S
In 1-th step the optimal policy are in L1 is C, in L2 is C, in L3 is S
In 2-th step the optimal policy are in L1 is C, in L2 is C, in L3 is S
In 3-th step the optimal policy are in L1 is C, in L2 is C, in L3 is S
In 4-th step the optimal policy are in L1 is C, in L2 is C, in L3 is S