编译原理（三）语法分析：5.自上而下语法分析

---

【编译原理博客列表】》》》》》》

---

一、自上而下分析的一般方法

1.描述

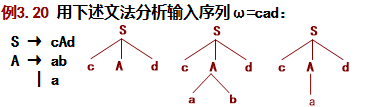
用推导的方法分析输入序列（记号流）：
对任何一个输入序列ω，从S开始进行最左推导，直到得到一个合法的句子或发现一个非法结构。
在推导的过程中，从左到右扫描输入序列，并试图用一切可能的方法，自上而下建立它的分析树。
自上而下分析是一种试探的过程，是反复使用不同产生式谋求与输入序列匹配的过程。

2.问题

• 公共左因子：若有A→αβ1|αβ2，则会虚假匹配和大量回溯；造成分析效率低、语义动作难以恢复、以及出错位置的报告不确切等。
• 左递归：若有A→Aα，则死循环使分析无法进行下去。

二、消除左递归

1.定义

定义3.9
若文法G中的非终结符A，对某个文法符号序列α存在推导A=+>Aα，则称G是左递归的。若G中有形如A→Aα的产生式，则称该产生式对A直接左递归。

2.消除直接左递归

（1）算法3.1 消除直接左递归

• 输入：G中所有的A产生式(含直接左递归)
• 输出：等价的不含直接左递归的G’
• 方法：

1. 首先，整理A产生式为如下形式：
   $A\to A{\alpha }_1|A{\alpha }_2|...|A{\alpha }_m|{\beta }_1|{\beta }_2|...|{\beta }_n$
   其中αi非空，βj均不以A开始。
2. 然后用下述产生式代替A产生式：
   $A\to {\beta }_1{A}^{\prime }|{\beta }_2{A}^{\prime }|...|{\beta }_n{A}^{\prime }$
   $A^{\prime }\to {\alpha }_1{A}^{\prime }|{\alpha }_2{A}^{\prime }|...|{\alpha }_m{A}^{\prime }|\epsilon$

例如：
考虑：$A\to A\alpha |\beta$，产生的语言：$\beta \alpha ?$
替换为：$A\to \beta A^{\prime }$，$A^{\prime }\to \alpha A^{\prime }|\epsilon$

注意：ε也算，如$A\to A\alpha |\beta |\epsilon$，替换为$A\to \beta A^{\prime }|A^{\prime }$，$A^{\prime }\to \alpha A^{\prime }|\epsilon$

（2）例子

例3.17 用算法3.1消除算术表达式文法的直接左递归：

2.消除左递归

（1）算法3.2 消除左递归

• 输入：无回路文法G
• 输出：无左递归的等价文法G’
• 方法：

1. 将非终结符合理排序：A1，A2，…，An;

for i in 2..n 
loop for  j in 1..i-1loop①用Aj→δ1|δ2|...|δk的右部替换每个形如Ai→Ajγ产生式中的Aj,得到新产生式：Ai→δ1γ|δ2γ|...|δkγ;②消除Ai产生式中的直接左递归;end loop; 
end loop;

核心思想：将左递归产生式（不是直接左递归的非终结符）右部展开（即替换左部）到其他产生式中

注意：若G产生句子的过程中出现A=>+A的推导，则无法消除左递归

（2）例子

例3.18 用算法3.2消除文法S→Aa|b，A→Ac|Sd|ε中的左递归。

① 将S的右部展开在A中，得到：
A→Ac|Aad|bd|ε
② 消除新产生式中的直接左递归，得到：
S→ Aa | b
A→ bdA' | A'
A'→ cA' | adA' | ε

三、提取左因子

1.算法3.3 提取文法的左因子

• 输入：文法G
• 输出：等价的无左因子文法G’
• 方法：

重复下述过程，直到所有A产生式候选项中不再有公共前缀

1. 重排A产生式：$A\to \alpha {\beta }_1|\alpha {\beta }_2|...|\alpha {\beta }_n|\gamma$；
2. 并用 $A\to \alpha A^{\prime }|\gamma$ 和 $A^{\prime }\to {\beta }_1|{\beta }_2|...|{\beta }_n$ 取代原A产生式。

注意：既有左递归又含左因子？先消除左递归。

2.例子

例3.20 考察悬空else文法：S→iCtS|iCtSeS|a，C→b

S→iCtSS'|a
S'→ε|eS
C→b

四、递归下降分析

1.概念

一个非终结符是一个子程序

1. 直接以程序的方式模拟产生式产生语言的过程；
2. 每个产生式对应一个子程序，产生式右边的非终结符对应子程序调用，终结符则与输入序列匹配；
3. 它对文法的限制是不能有公共左因子和左递归；
4. 它是一种非形式化的方法，只要能写出子程序，用什么样的方法和步骤均可。

2.方法

1. 消除文法中的公共左因子和左递归
2. 构造文法的状态转换图并且化简
3. 将转换图转化为EBNF表示；
4. 从EBNF构造子程序。

（1）文法的状态转换图：每个非终结符对应一个状态转换图

• 为非终结符A建立一个初态和一个终态；
• 为A→X1X2…Xn构造从初态到终态的路径，边标记为X1，X2，…，Xn。
• 根据识别同一集合的原则，化简转换图。

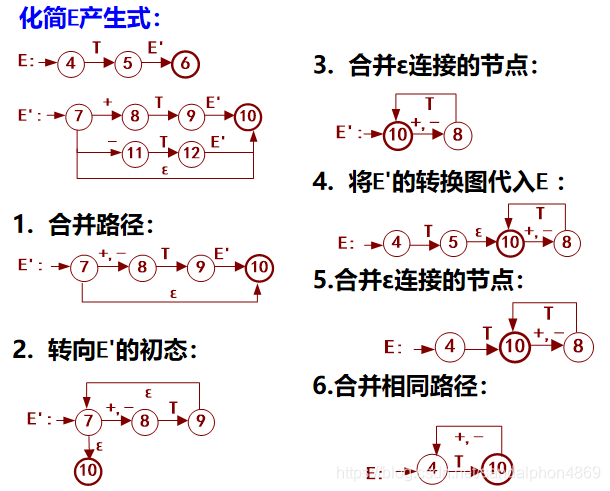
（2）状态图的化简

• 标记相同的路径可以合并；
• 标记为A的边可等价为标记ε的边转向A转换图的初态；
• ε边连接的两个状态可以合并；
• 不可区分的状态可以合并。

（3）文法的扩展BNF（EBNF）表示

① { }：重复0或若干次（while）
② [ ]：可选择（if或while）
③ |：括弧( )之内的或关系（case）
④ ( )：改变运算的优先级和结合性

3.例

递归下降分析的文法：
L→E;L|ε
E→E+T|E-T|T
T→T*F|T/F|T mod F|F
F→(E)|id|num

（1）消除左递归后的等价文法:

L →E;L|ε
E →TE'
E'→+TE'|-TE'|ε
T →FT'
T'→*FT'|/FT'| mod FT'|ε
F →(E)|id|num 

（2）构造文法的状态转换图并且化简

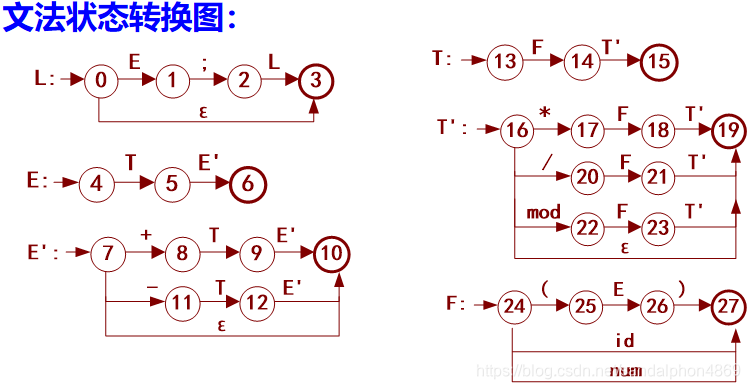
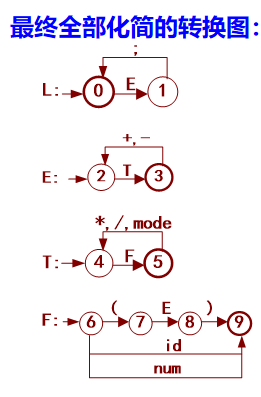
（3）文法的扩展BNF（EBNF）表示

L → {
     E; }
E → T {
     (+|-) T }
T → F {
     (*|/|mod) F }
F → ( E ) | id | num