曲线拟合(1)——Logistic曲线

To be continue … …

这是创新训练传染病的微分方程模型Logistic曲线笔记

一、Logistic模型

1.1 Logistic方程概述

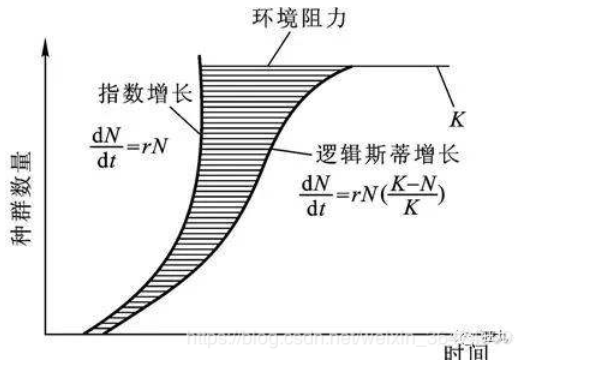
图1

Logistics方程可用下列微分方程描述
$\begin{aligned} \begin{cases} \displaystyle \frac{\mathrm{d}N}{\mathrm{d}t}=r\big(1-\frac{N}{N_{m}}\big)N\\ N(t_{0})=N_{0} \end{cases}\tag{1} \end{aligned}$

变量分离方程，其中 $N_{m}$表示理论上的最大值， $N_{0}$表示 $t_{0}$时刻的病人数

分离变量，得
$\frac{\mathrm{d}N}{(1-\frac{N}{N_{m}})\frac{N}{N_{m}}}=rN_{m}\mathrm{d}t$
即
$\frac{1}{N}\mathrm{d}N-\frac{1}{N_{m}-N}\mathrm{d}(N_{m}-N)=r\mathrm{d}t$
也就是
$\begin{aligned} &\ln N-\ln(N_{m}-N)=rt+C'\\ &\Rightarrow \ln(\frac{N}{N_{m}-N})=rt+C'\\ &\Rightarrow \frac{N}{N_{m}-N}=C\mathrm{e}^{rt}(其中,C=\mathrm{e}^{C'})\\ &\Rightarrow N=\frac{N_{m}}{1+1/C\cdot\mathrm{e}^{-rt}} \end{aligned}$
代入初值条件 $N(t_{0})=N_{0}$，得
$C=\frac{N_{0}}{N_{m}-N_{0}}\mathrm{e}^{-rt_{0}}$
代入上式得
$\begin{aligned} & N=\frac{N_{m}}{1+(\frac{N_{m}}{N_{0}}-1)\mathrm{e}^{-r(t-t_{0})}}\\ & \Rightarrow N=\frac{1}{\frac{1}{N_{m}}+(\frac{1}{N_{0}}-\frac{1}{N_{m}})\mathrm{e}^{-r(t-t_{0})}}\tag{2} \end{aligned}$

由上式可看出，令 $t\to\infty$， $N\to N_{m}$，也即
$N=\frac{N_{0}N_{m}\mathrm{e}^{r(t-t_{0})}}{N_{0}(\mathrm{e}^{r(t-t_{0})}-1)+N_{m}}$

另外一种形式的logistic微分方程如下

$\begin{aligned} \begin{cases} \displaystyle \frac{\mathrm{d}N}{\mathrm{d}t}=rN-kN^{2}\\ N(t_{0})=N_{0} \end{cases}\tag{3} \end{aligned}$

其中， $r$表示发病率， $k$表示预防效果

同理即得
$N=\frac{1}{\frac{k}{r}+(\frac{1}{N_{0}}-\frac{k}{r})\mathrm{e}^{-r(t-t_{0})}}$

其中， $N_{m}=\frac{r}{k},(while\ t\to\infty)$，表示理论上的最大人数

1.2 Logistic方程的性质

图2

由 $\frac{\mathrm{d}N}{\mathrm{d}t}=-kN^{2}+rN$的右端函数，不妨设为 $f(N)$，则

易知 $f>0$对 $N\in(0,N_{m})$恒成立，函数图像为开口向下的抛物线

也就是 $\frac{\mathrm{d}N}{\mathrm{d}t}>0$对 $N\in(0,N_{m})$恒成立，也即 $N(t)$在 $(0,N_{m})$单调递增

又因为 $f'=-2kN+r$，即 $f'(N_{m}/2)=0$；当 $N<\frac{N_{m}}{2}$时， $f'>0$，当 $N>\frac{N_{m}}{2}$时， $f'<0$。即表明当 $N<\frac{N_{m}}{2}$时，增长率 $\frac{\mathrm{d}N}{\mathrm{d}t}$是增加的，当 $N>\frac{N_{m}}{2}$时，增长率是减小的。在 $N=\frac{N_{m}}{2}$时，增长率 $\frac{\mathrm{d}N}{\mathrm{d}t}$达到最大。可看成疫情拐点的到来。且当 $t\to\infty$时， $N\to N_{m}$。

由上式，代入 $N=\frac{N_{m}}{2}$，求得时间 $t$，即
$t=\frac{1}{r}\ln(\frac{N_{m}}{N_{0}}-1)+t_{0}=\frac{1}{r}\ln(\frac{r}{kN_{0}}-1)+t_{0}\tag{4}$

即为疫情出现拐点的可能时间 $t$。

二、Logistic曲线拟合方法

对于logistic曲线的参数拟合方法，见参考文献

---

• Matlab拟合logistic曲线

• Wikipedia Logistic function

• python实现logistic增长模型拟合2019-nCov确诊人数2月1日更新

---

拟合的初值选取方法等

2.1 Logistic曲线初值的选取

对于如下一组数据

表1

序号	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
日期	11	18	19	20	21	22	23	24	25	26	27	28	29	30	31
感染人数	41	45	62	291	440	571	830	1287	1975	2744	4515	5974	7711	9692	11791

用logistic曲线拟合

用形如 $A/(1+b\mathrm{e}^{-ct})$拟合

1. Matlab拟合

clear
clc
x=1:15;
y=[41,45,62,291,440,571,830,1287,1975,2744,4515,5974,7711,9692,11791];
% syms b c
% [b,c]=solve(5000/(1+b*exp(-c*1))==43,5000/(1+b*exp(-c*2))==45,b,c)
c0=[5000,120.6896,0.0459];
% c0=[6000 145.0271 0.0458];c0=[10000 242.3770 0.0457];
fun=inline('c(1)./(1+c(2).*exp(-c(3).*x))','c','x');
b=nlinfit(x,y,fun,c0);disp("各参数的值(c(1) c(2) c(3)):");disp(b);
t=0:0.1:30;
plot(x,y,'rs',t,fun(b,t),'b');set(gca,'ygrid','on');
legend("真实值","预测曲线");xlabel("日数");ylabel("累计病人数");

对于A的初值选取，可任意选取 $A_{0}=5000$，将初值 $F(1)=43,F(2)=45$代入

syms b c
[b,c]=solve(5000/(1+b*exp(-c*1))==43,5000/(1+b*exp(-c*2))==45,b,c)

解得： $C_{0}=[5000,b,c]$

即得logistic方程如下
$N=\frac{17715}{1+473\cdot\mathrm{e}^{-0.4553t}}$

图3

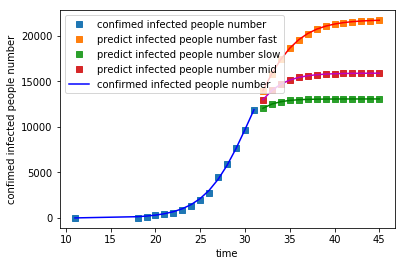
2. python拟合

一般来说， $r$越小，累计病人数增多，且结束的时间长；反之亦然

图4

2.2 Logistic曲线的参数拟合方法

主要参考文献

---

• 殷祚云.Logistic曲线拟合方法研究[J].数理统计与管理,2002(01):41-46.
• 主要包括(线性或非线性)：三点法、四点法和拐点法

---

Logistic方程为
$N=\frac{N_{m}}{1+\mathrm{e}^{b-rt}}\tag{5}$

其中，N为生物量，r为内禀自然增长率， $N_{m}$为环境容纳量，b为积分常数

将上式取对数，整理得
$\ln\frac{N_{m}-N}{N}=b-rt\tag{6}$

2.2.1 三点法

假设有实测数据 $Q=\left\{(t_{1},N_{1}),(t_{2},N_{2}),\cdots,(t_{n},N_{n})\right\}$，分别选取数据Q的始点、中点和终点数据，即 $A(T_{1},N_{T_{1}}),B(T_{2},N_{T_{2}}),(C_{T_{3},N_{T_{3}}})$，代入(6)得
$\begin{aligned} \begin{cases} \ln\frac{N_{m}-N_{1}}{N_{1}}=b-rT_{1}\ \ \ ① \\ \ln\frac{N_{m}-N_{2}}{N_{2}}=b-rT_{2}\ \ \ ② \\ \ln\frac{N_{m}-N_{3}}{N_{3}}=b-rT_{3}\ \ \ ③ \end{cases}\tag{7} \end{aligned}$
其中 $2T_{2}=T_{1}+T_{2}$，由①+③-2②整理得
$2\ln\frac{N-N_{T_{2}}}{N_{T_{2}}}=\ln\frac{N-N_{T_{1}}}{N_{T_{1}}}+\ln\frac{N-N_{T_{3}}}{N_{T_{3}}}$
化简得
$N_{m}(\frac{1}{N_{2}^{2}}-\frac{1}{N_{1}N_{3}})=-\frac{N_{1}+N_{3}}{N_{2}}+\frac{2}{N_{2}}$
整理得
$N_{m}=\frac{2N_{1}N_{2}N_{3}-N_{2}^{2}(N_{1}+N_{3})}{N_{1}N_{3}-N_{2}^{2}}\tag{8}$
如上对于表1数据，可取 $A(t_{初}=1,41),B(t_{{中}}=8,1287),C(t_{{终}}=15,11791)$，代入(2)式得 $N_{m}=15648$。此时对于(1)式用最小二乘法做线性拟合，即形如 $y=b-rt$。

最小二乘法估计公式：设有一列点 $(x_{i},y_{i}),i=1,2,\cdots,n$，利用 $y=ax+b$估计
$\begin{aligned} \begin{cases} \displaystyle \bar{a}=\frac{n\sum_{i=1}^{n}x_{i}y_{i}-(\sum_{i=1}^{n}x_{i})(\sum_{i=1}^{n}y_{i})}{n\sum_{i=1}^{n}x_{i}^{2}-(\sum_{i=1}^{n}x_{i})^{2}}\\\\ \displaystyle \bar{b}=\frac{(\sum_{i=1}^{n}x_{i}^{2})(\sum_{i=1}^{n}y_{i})-(\sum_{i=1}^{n}x_{i}y_{i})(\sum_{i=1}^{n}x_{i})}{n\sum_{i=1}^{n}x_{i}^{2}-(\sum_{i=1}^{n}x_{i})^{2}} \end{cases} \end{aligned}$

对于原始数据Q做变换得

表2

序号	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
变换后	5.9419	5.8486	5.5270	3.9660	3.5428	3.2735	2.8822	2.4122	1.9349	1.5481	0.9025	0.4820	0.0289	-0.4869	-1.1174

这是线性拟合

利用cftool线性最小二乘法拟合求得 $r=0.5042,b=6.4793$

clear
clc
t=1:15;
N=[41 45 62 291 440 571 830 1287 1975 2744 4515 5974 7711 9692 11791];
K=15648;
NN=log(K./N-1);
plot(t,N,'s');set(gca,'ygrid','on');
p=polyfit(t,NN,1)

2.2.2 四点法

假设有实测数据 $Q=\left\{(t_{1},N_{1}),(t_{2},N_{2}),\cdots,(t_{n},N_{n})\right\}$，分别选取数据Q的始点、中点两点和终点共四个数据，即 $A(T_{1},N_{1}),B(T_{2},N_{2}),C({T_{3},N_{3}}),D(T_{4},N_{4})$，代入(i)得，
$\begin{aligned} \begin{cases} \ln\frac{N_{m}-N_{1}}{N_{1}}=b-rT_{1}\ \ \ ? \\ \ln\frac{N_{m}-N_{2}}{N_{2}}=b-rT_{2}\ \ \ ?\\ \ln\frac{N_{m}-N_{3}}{N_{3}}=b-rT_{3}\ \ \ ? \\ \ln\frac{N_{m}-N_{4}}{N_{4}}=b-rT_{4}\ \ \ ? \end{cases}\tag{9} \end{aligned}$
其中 $T_{1}+T_{4}=T_{2}+T_{3}$，由 $?+?-?-?$得
$\ln\frac{N_{m}-N_{2}}{N_{2}}+\ln\frac{N_{m}-N_{3}}{N_{3}}=\ln\frac{N_{m}-N_{1}}{N_{1}}+\ln\frac{N_{m}-N_{4}}{N_{4}}$
整理得
$N_{m}(\frac{1}{N_{2}N_{3}}-\frac{1}{N_{1}N_{4}})=\frac{N_{2}+N_{3}}{N_{2}N_{3}}-\frac{N_{1}+N_{4}}{N_{1}N_{4}}$
即
$N_{m}=\frac{N_{1}N_{4}(N_{2}+N_{3})-N_{2}N_{3}(N_{2}+N_{3})}{N_{1}N_{4}-N_{2}N_{3}}\tag{10}$
同理，对于表1的数据，可取 $A(t_{{初}}=1,41),B(t=6,571)$， $C(t=10,2744)$， $D(t_{{终}}=15,11791)$，计算可得 $N_{m}=15632$。此时对于(1)式用最小二乘法做线性拟合

2.2.3 拐点法

拐点的另外一种求法

对于方程
$\frac{\mathrm{d}N}{\mathrm{d}t}=r(1-\frac{N}{N_{m}})N$
左右两边对 $t$求导数，即
$\frac{\mathrm{d}^{2}N}{\mathrm{d}t}=r(1-\frac{2N}{N_{m}})\frac{\mathrm{d}N}{\mathrm{d}t}\tag{12}$

当 $\frac{\mathrm{d}N}{\mathrm{d}t}\neq0$时，即得 $\frac{\mathrm{d}^{2}N}{\mathrm{d}t}=0\Rightarrow N=\frac{N_{m}}{2}$，即当 $\frac{\mathrm{d}N}{\mathrm{d}t}$最大时，也就是曲线斜率最大处时 $N_{k}=\frac{N_{m}}{2}$，即 $N_{m}=2N_{k}$。曲线由凸变凹。

2.2.4 误差估计——决定系数

一个特定数值对于其平均值的偏离，称为离差。决定系数的定义公式为
$R^{2}=\frac{SSR}{SST}=\frac{\sum(\hat{y}-\bar{y})^{2}}{\sum(y-\bar{y})^{2}}=1-\frac{\sum(y-\hat{y})^{2}}{\sum(y-\bar{y})^{2}}$

2.2.5 非线性拟合

任意取A的一个初值 $A_{0}$，然后利用两个方程求解另两个参数的初值

syms b c
[b,c]=solve(5000/(1+b*exp(-c*1))==43,5000/(1+b*exp(-c*2))==45,b,c)

然后用L-M方法据梯度降速求得最优参数。

三、Logistic预测增长