近似算法——续

树上的独立集

关键：如果一个节点是叶子节点，则树上其中的一个最大独立集一定包含该节点。
证明：考虑叶子节点$v$与其父亲节点$u$，若两个都不属于最大独立集，则我们可以将叶子节点加入形成一个更大的独立集；如果只有叶子节点不属于，那么我们可以选择不将父亲节点加入而将叶子节点加入独立集，此时仍是一个最大独立集。
树上的贪心策略
如果树中还存在一条边，则将该边中属于叶子的节点$v$加入最大独立集，删除两个顶点以及这两个顶点所邻接的所有边。重复上述操作，直到树中不存在边，所得集合为树的最大独立集。

树上带权独立集

关键：树中各子树之间没有直接联系，因此可以动态规划求解

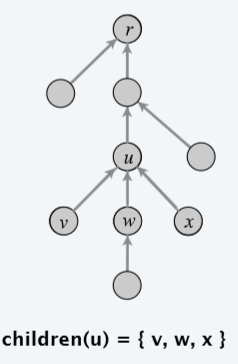
分情况说明：

• 最大带权独立集为包含根节点，则与其连接的子树的根节点不能选择
• 最大带权独立集为不包含根节点，则与其连接的子树的根节点可以选，当然也可以不选，取选和不选中最大的。

目标：max{OPTin(r),OPTout(r)}max\{OPT_{in}(r),OPT_{out}(r)\}max{ OPTin?(r),OPTout?(r)}，其中：

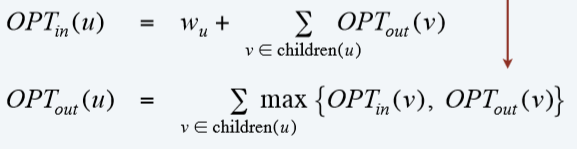
顶点覆盖问题

2倍近似算法：任意选一个边，将该边的两个端点加入近似的顶点覆盖集合中，将该边加入近似匹配中，删除与这两个端点邻接的所有边。重复上述过程，直到图中不存在边为止。

贪心算法得到的顶点覆盖是二倍近似的，即$S\le 2|S^{?}|$
证明：

• $S$是一个顶点覆盖，因为只有该边被覆盖了才会被删除，最后所有边都被删除，证明所有边都被$S$集合覆盖。
• $M$是一个匹配，$M$中的边加入$M$后，所有与该边两个顶点相连的边都会被删除，所以$M$中不存在两个边拥有相同顶点
• $S=2M\le 2|S^{?}|$，因为$M$中任意两条边之间不存在公共端点，所以覆盖完$M$中的边至少需要|M|个顶点，所以$S^{?}\ge M$

贪心算法得到的匹配是二倍近似的，即$|M|\ge \frac{1}{2}|M^{?}|$
$|M|=\frac{1}{2}|S|\ge \frac{1}{2}|M^{?}|$，还是因为$M^{?}$中任意两条边之间不存在公共端点，所以覆盖完$M^{?}$中的边至少需要$|M^{?}|$个顶点，而任意一个顶点覆盖是要覆盖完所有边的，因此$|S|\ge |M^{?}|$