近似算法_综合

负载均衡问题

问题描述：有 $m$ 个机器， $n$ 个任务，任务 $j$ 的处理时间为 $t_j$ ，每个任务只能在一台机器上连续工作，一台机器同一时间只能处理一个任务。
机器 $i$ 的负载： $\sum_{j\in S[i]}t_j$ ， $S [i]$ 为分配给机器 $i$ 的任务集合
工期： $L=max_iL[i]$
优化问题：寻找一个分配方案最小化工期
决策问题：是否存在一个分配方案使工期为 $L$

负载均衡问题是NPH问题，让分割问题 $≤p\leq_p$ 负载均衡问题
构造思路：
任给分割问题的实例 $v1,v2,…,vnv_1,v_2,\dots,v_n$ ，我们构造3负载均衡的实例，即共有3台机器工作。任务 $t1=v1,t2=v2,…,tn=vn，tn+1=12∑ivit_1 = v_1,t_2=v_2,\dots,t_n=v_n，t_{n+1} = \frac{1}{2}\sum_iv_i$ 。分割问题有解当且仅当3-负载均衡问题存在工期为 $12∑ivi\frac{1}{2}\sum_iv_i$ 的分配方案。

①负载均衡的2倍近似算法
贪心思路：不用排序，将任务分配给当前工期最小的机器上
两个结论

最优工期 $L?≥maxjtjL^*\geq max_jt_j$ （总有一个机器要处理这个最大时间的任务）
最优工期 $L?≥1m∑jtjL^*\geq \frac{1}{m}\sum_jt_j$ （最优工期大于等于绝对平衡工期）

2倍近似度证明：

设机器 $i$ 是瓶颈机器(则 $L [i]$ 为贪心解)，任务 $j$ 是最后一个在机器 $i$ 上调度的任务（在调度前，机器 $i$ 的工期是最小的）
$-t_j \leq L[k]$ ，对任意 $1≤k≤m1\leq k \leq m$

$-t_j \leq \frac{1}{m}\sum_kL[k] = \frac{1}{m}\sum_jt_j\leq L^*$

$(L[i]-t_j)+t_j\leq 2L^*$

2倍界是紧的，我们可以构造一个例子，最大极限为2。
如： $m$ 个机器，m(m-1)个长度为1的任务，1个长度为 $m$ 的任务
在这里插入图片描述

极限： $limm→∞2m?1m=2lim_{m\rightarrow \infty}\frac{2m-1}{m}=2$

②负载均衡的 $43\frac{4}{3}$ 倍近似算法
贪心思路：按照处理时长由大到小排序，将排序后的任务依次分配给当前工期最小的机器上。
我们只证明该算法是 $32\frac{3}{2}$ 倍近似的

如果瓶颈机器只有一个任务，那么我们的算法得到的分配方案是最优的
如果瓶颈机器有两个及以上个任务（说明每个机器都至少有一个任务，不然需把瓶颈机器最后一个任务安排到空机器上），则 $L?≥2tm+1L^*\geq 2t_{m+1}$ （瓶颈机器至少要做两个任务，两个任务的时间总和 $≥2tm+1\geq 2t_{m+1}$ ）

于是我们只需证明在瓶颈机器有两个及以上个任务时，得到的解是 $32\frac{3}{2}$ 倍近似的即可
仍设任务 $j$ 是瓶颈机器 $i$ 最后处理的任务，在瓶颈机器有两个及以上个任务时， $tj≤tm+1t_j\leq t_{m+1}$ ， $L?≥2tm+1≥2tjL^*\geq 2t_{m+1}\geq 2t_j$ ， $tj≤12L?t_j\leq\frac{1}{2}L^*$

因此： $L=L[i]=(L[i]?tj)+tj≤32L?L=L[i]=(L[i]-t_j)+t_j\leq \frac{3}{2}L^*$

$32\frac{3}{2}$ 倍近似不是紧的， $43\frac{4}{3}$ 倍近似才是紧的，例子如下：
$m$ 个机器， $n = 2 m + 1$ 个任务，长度为 $m,m+1,…,2m?1m,m+1,\dots,2m-1$ 的任务各两个，长度为 $m$ 的任务1个。
$LL?=4m?13m,limm→∞4m?13m=43\frac{L}{L^*} = \frac{4m-1}{3m},lim_{m\rightarrow\infty} \frac{4m-1}{3m}=\frac{4}{3}$

中心选择问题

问题描述：给定 $n$ 个站点，寻找 $k$ 个中心，每个站点距自身最近中心的距离为 $dist(s_i,C)$ ，问一种中心选择方案，使最大的 $dist(s_i,C)$ 尽可能的小。

几个符号标注：
$d i s t (x, y)$ ：站点 $x$ 和 $y$ 之间的距离
$dist(si,C)=minc∈Cdist(si,c)dist(s_i,C) = min_{c\in C}dist(s_i,c)$ ： $s_i$ 到其最邻近中心的距离
$r(C) = max_i dist(s_i,C)$ ：最小覆盖半径

贪心策略：选择与当前存在的一系列中心最远的站点作为下一个中心（一开始随机选一个站点作为中心集合的第一个点）
启发式思想：每个站点尽可能分离，覆盖范围尽可能的分离，有效利用覆盖半径。

证明该算法是一个二倍近似算法，即 $r(C)≤2r(C?)r(C)\leq 2r(C^*)$
在这里插入图片描述
反证法，假设 $r(C?)<12r(C)r(C^*)<\frac{1}{2}r(C)$

对于贪心选择的中心 $ci∈Cc_i\in C$ ，考虑其半径为 $12r(C)\frac{1}{2}r(C)$ 的区域
在每个区域中有且仅有一个最优中心 $c_i^*$ （若区域中不存在最优中心，则找到一个站点与最优站点距离大于 $12r(C)\frac{1}{2}r(C)$ ，与假设矛盾；若存在两个以上，则一定有一个区域不存在最优中心），令贪心解 $c_i$ 与 $c_i^*$ 对应。
取任意站点 $s$ ， $c_i^*$ 为站点 $s$ 在最优解中的最近中心， $dist(s,C)≤dist(s,ci)≤dist(s,ci?)+dist(ci,ci?)≤2r(C?)dist(s,C)\leq dist(s,c_i)\leq dist(s,c_i^*)+dist(c_i,c_i^*)\leq 2r(C^*)$

因此： $r(C)≤2r(C?)r(C)\leq 2r(C^*)$
除非 $P = N P$ ，否则中心选择问题不存在2倍近似度以下的算法

带权顶点覆盖问题

问题描述：在顶点覆盖的条件下，满足所选顶点总权重之和最小
在这里插入图片描述
①竞价法
给每个边赋予一个价格 $pe≥0p_e\geq0$ ，任意顶点的权重大于等于与其邻接的所有边价格总和：
$∑e=(i,j)pe≤wi\sum_{e=(i,j)}p_e\leq w_i$
公平引理：对于任意顶点覆盖集合 $S$ 和任意公平价格 $p_e$ ，有 $∑epe≤w(S)\sum_e p_e\leq w(S)$
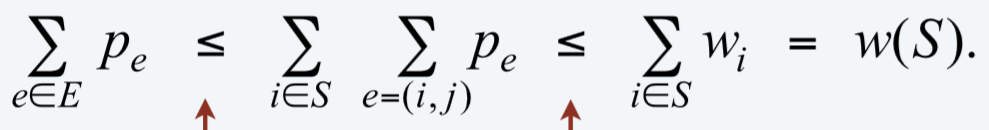
在这里插入图片描述
贪心策略：只要存在一条边 $e (i, j)$ 其两个端点都未饱和，则增加该边的价格，直到其中一个端点饱和为止。重复上述操作，直到找不到满足上述的边为止。

证明竞价法是一个二倍近似算法：
令 $S$ 为贪心算法终止时，所有饱和顶点的集合，易得 $S$ 为一个顶点覆盖（反证，如果某条边没有被覆盖到，则其两个端点都未饱和，算法不会终止）
证明关键： $∑e∈Epe≤w(S?)\sum_{e\in E}p_e\leq w(S^*)$
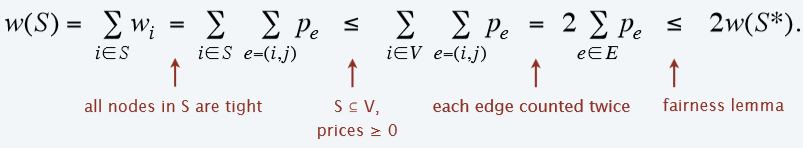
在这里插入图片描述

②线性规划方法近似
带权顶点覆盖问题可以转化为整数线性规划问题
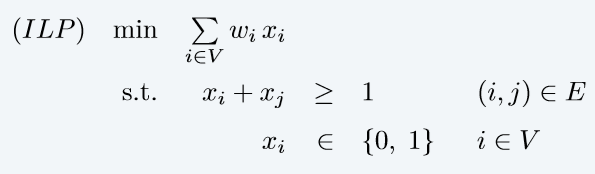
在这里插入图片描述
顶点覆盖问题 $?\Leftrightarrow$ 带权顶点覆盖（权重设为1） $?\Leftrightarrow$ 整数线性规划（ $w_i=1$ ）
如果我们能多项式时间解整数线性规划，则我们能多项式时间解带权顶点覆盖问题，但是整数线性规划是 $N P H$ 的，而一般线性规划可以多项式时间求解，因此我们用一般线性规划去近似整数线性规划的解。
证明线性规划的解取整是2倍近似的
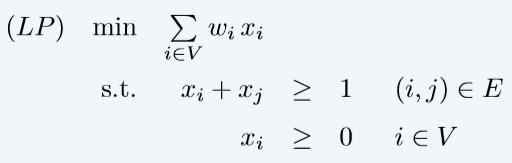
在这里插入图片描述
设 $x$ 是线性规划的最优解，集合 $S={i∈V:xi≥12}S=\{i\in V:x_i\geq \frac{1}{2}\}$ 是一个顶点覆盖，且权重不超过最优顶点覆盖权重的2倍

证明集合 $S$ 是一个顶点覆盖：对任意一条边 $(i, j)$ ，由于 $xi+xj≥1x_i+x_j\geq 1$ ，因此至少有一个值 $≥12\geq\frac{1}{2}$ ，即至少有一个端点在集合 $S$ 中，因此集合 $S$ 是一个顶点覆盖。
集合 $S$ 权重不超过最优顶点覆盖权重的2倍：
$∑i∈S?wixi?≥∑i∈Swixi≥12∑i∈Swi\sum_{i\in S^*}w_ix_i^*\geq \sum_{i\in S}w_ix_i\geq\frac{1}{2}\sum_{i\in S}w_i$

中间项为没有整数限制的一般线性规划的解（没有近似的），最后一项表示近似后的权重和
除非 $P = N P$ ，不然没有近似度<1.3606的算法，即使所有权重都设为1

一般化的负载均衡

问题描述：增加了任务只能在授权机器上进行处理，仍然是一个任务只能在一台机器上连续工作，求最小化工期的任务分配方案
一般化的负载均衡可以与整数线性规划等价，当用一般线性规划近似时，问题含义会发生变化，即一个任务可以分成多片在不同授权机器上运行
$x_{ij}$ 表示机器 $i$ 处理任务 $j$ 所用的时间
在这里插入图片描述
根据上述一般线性规划的解 $x$ ，我们可以构造一个无环图 $G$ 。如果 $G$ 有环，我们也可以通过流转换的形式，将其转换成一个等价的无环图的形式。
构造思路：选任意一个机器作为根节点，若 $x_{ij}>0$ ，则机器 $i$ 和任务 $j$ 之间存在一条边。
从上述无环图中，我们按照以下规则得到近似的分配方案（相当于线性规划的取整操作）：

如果任务 $j$ 是叶子节点，则将其分配给父亲节点的机器 $i$ （相当于单授权节点）
如果任务 $j$ 是非叶子节点，则将其分配给它随机的一个孩子节点机器（相当于可多授权节点）

两个事实：

任意一个任务的处理时长小于等于最优工期，即 $tj≤L?t_j\leq L^*$ ，因为 $tj≤maxjtj≤L?t_j\leq max_jt_j\leq L^*$
因为最大时间的任务总要被某个机器处理，工期至少为最大时间的任务
叶子节点，表示能够处理该任务的机器只有一台，因此线性规划对应的解 $x_{ij}=t_j$ ，因为需要满足 $∑ixij=tj\sum_i x_{ij} = t_j$ ，且只有一项参与求和。

对于叶子结点：
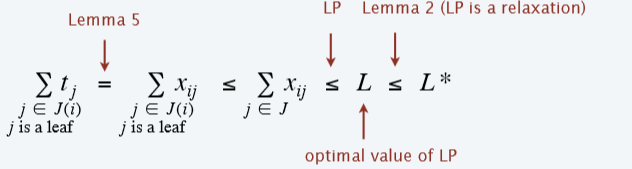
在这里插入图片描述
对于非叶子节点：

综上全局负载： $Li≤2L?L_i \leq 2L^*$

补充：通过流思想将有环图转化成无环图
将 $x_{ij}$ 看成任务 $j$ 流向机器 $i$ 的流，任务指向机器的链路容量设置为 $∞\infty$ ，机器节点到宿点的链路容量设置为 $L$ ，即最大工期。每个任务节点 $j$ 的出口流量之和为 $t_j$ ，最终流入宿点的总流量为 $∑jtj\sum_jt_j$
在这里插入图片描述
如果存在环，则删除环中的一条边，调整流量（二部图抵消原则）依然满足原线性规划的约束，知道图中不存在环为止。

运行时间：
对于线性规划而言，我们需要 $x_{ij}$ 和 $L$ ，因此一共 $m n + 1$ 个变量。
对于流网络而言，我们需要 $m + n + 1$ 个节点，然后运行流算法

01背包问题

两种思路：

枚举物品集合、重量上限下的最大价值，一直枚举到 $n$ 个物品和最大重量，此时对应的最大价值为目标解
枚举物品集合、价值下限下的最小重量，一直枚举到 $n$ 个物品和满足重量约束下的最小价值，此时对应的价值为目标解

①状态转移方程
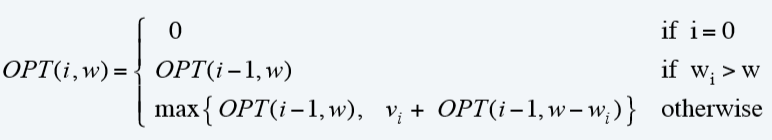
在这里插入图片描述
最大能达到的重量为 $W$ ，最优的时间复杂度为 $O (n W)$

②状态转移方程
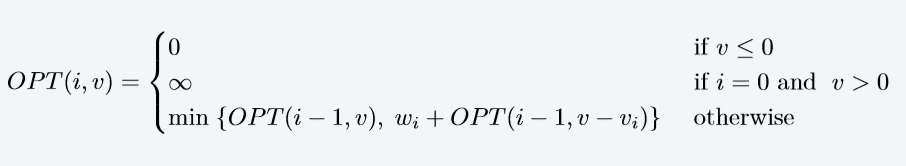
在这里插入图片描述
最大能达到的价值数为 $nv_{max}$ ，因此计算复杂度为 $O(n^2v_{max})$

针对目标②我们给出相应的近似算法：
近似原则：

$0<?<10<\epsilon<1$ ：定义为近似程度
$v_{max}$ 是 $n$ 个物品中最大的价值
$θ\theta$ 是放缩因子，是跟近似程度正相关的参数，定义为 $θ=?vmax2n\theta = \frac{\epsilon v_{max}}{2n}$ ，形象理解为含 $k$ 个0近似的大整数， $k$ 越大越粗糙，精度损失越大。
若原物品价值为 $v_i$ ，则近似价值为 $vi?=?viθ?θ\overline{v_i} = \lceil\frac{v_i}{\theta}\rceil \theta$ ，缩小相同倍数得到等价价值 $?viθ?\lceil\frac{v_i}{\theta}\rceil$

我们的近似算法相当于对大价值数进行向上凑整，因此恰好等于重量约束时，会比最优解的价值总和大一些，当然比非最优解大更多。大的程度跟凑整时的近似程度有关。下式非常直观：表示近似物品价值向上凑整后大于任意可行解（最优解是可行解中最大的那个，可以直接替换成最优解）。其中的价值都是没有近似的价值，近似算法得到的只是一个物品集合，不修改原价值：
$(1+?)∑i∈Svi≥∑i∈S?vi(1+\epsilon)\sum_{i\in S}v_i \geq \sum_{i\in S^*}v_i$

证明过程关键步骤在如何替换 $θ\theta$ （ $θ\theta$ 的定义）以及如何替换 $v_{max}$ （任意解集合只放最大价值物品带入不等式）
在这里插入图片描述

近似算法时间复杂度
原先复杂度为 $O(n2v^max)O(n^2\widehat{v}_{max})$ ，又 $v^max=?vmaxθ?=?2n??\widehat{v}_{max} = \lceil \frac{v_{max}}{\theta}\rceil = \lceil\frac{2n}{\epsilon} \rceil$ ，因此最优的时间复杂度为 $O(n3?)O(\frac{n^3}{\epsilon})$