【运筹学】线性规划单纯形法 ( 案例解析 | 标准形转化 | 查找初始基可行解 | 最优解判定 | 查找入基变量与出基变量

文章目录

一、线性规划示例
二、转化成标准形式
三、初始基可行解
四、列出单纯形表
五、计算检验数
六、选择入基变量与出基变量
七、第一次迭代 : 列出单纯形表

一、线性规划示例

线性规划示例 : 使用单纯形法求解下面的线性规划 ;

$\begin{array}{lcl} max Z = x_1 + 2x_2 + x_3 \\ \\ s.t\begin{cases} 2 x_1 - 3x_2 + 2x_3 \leq 15 \\\\ \dfrac{1}{3}x_1 + x_2 + 5x_3 \leq 20 \\ \\x_j \geq 0 & (j = 1 , 2 , 3 ) \end{cases}\end{array}$

二、转化成标准形式

首先将现行规划转化成标准形式 :

1 . 处理约束变量 : 所有的约束变量都大于等于 $0$ , 这里无需处理 ;

2 . 将不等式转为等式 : 两个不等式都是小于等于不等式 , 在左侧加入松弛变量即可 ;

① 添加松弛变量 : 上述两个不等式 $\begin{cases} 2 x_1 - 3x_2 + 2x_3 \leq 15 \\\\ \dfrac{1}{3}x_1 + x_2 + 5x_3 \leq 20 \end{cases}$ , 在左侧分别添加 $x_4 , x_5$ 松弛变量 ;

② 最终结果 : 转化后的结果是 $\begin{cases} 2 x_1 - 3x_2 + 2x_3 + x_4 = 15 \\\\ \dfrac{1}{3}x_1 + x_2 + 5x_3 + x_5 = 20 \\ \\x_j \geq 0 \quad (j = 1 , 2 , 3, 4, 5 ) \end{cases}$

3 . 处理目标函数取最大值 : 目标函数就是取最大值 , 无需处理 ;

4 . 最终的标准形结果是 :

$\begin{array}{lcl} max Z = x_1 + 2x_2 + x_3 + 0x_4 + 0x_5 \\ \\ s.t\begin{cases} 2 x_1 - 3x_2 + 2x_3 + x_4 + 0x_5 = 15 \\\\ \dfrac{1}{3}x_1 + x_2 + 5x_3 + 0x_4 + x_5 = 20 \\ \\x_j \geq 0 \quad (j = 1 , 2 , 3, 4, 5 ) \end{cases}\end{array}$

三、初始基可行解

找初始基可行解 :

① 查找单位阵 : 该线性规划标准形的系数矩阵中 , $x_4 , x_5$ 的系数矩阵是 $\begin{pmatrix} \quad 1 \quad 0 \quad \\ \quad 0 \quad 1 \quad \\ \end{pmatrix}$ , 该矩阵是单位阵 ;

② 可行基 : 选择该矩阵作为可行基 ;

③ 初始基可行解 : 其对应的解是基可行解 $\begin{pmatrix} \quad 0 \quad \\ \quad 0 \quad \\ \quad 0 \quad \\ \quad 15 \quad \\ \quad 20 \quad \\ \end{pmatrix}$ ;

四、列出单纯形表

$c_j$	$c_j$		$1$	$2$	$1$	$0$	$0$
$C_B$ 基变量系数 (目标函数)	基变量	常数 $b$	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$	$\theta_i$
$0$ ( 目标函数 $x_4$ 系数 $c_4$ )	$x_4$	$15$	$2$	$-1$	$2$	$1$	$0$	$-$
$0$ ( 目标函数 $x_5$ 系数 $c_5$ )	$x_5$	$20$	$\dfrac{1}{3}$	$1$	$5$	$0$	$1$	$20$
$\sigma_j$ ( 检验数 )			$1$ ( $\sigma_1$ )	$2$ ( $\sigma_2$ )	$1$ ( $\sigma_3$ )	$0$	$0$

五、计算检验数

计算非基变量的检验数 :

单个检验数计算公式 : $\sigma_j = c_j - \sum c_i a_{ij}$ , 其中 $c_j$ 是对应目标函数非基变量系数 , $c_i$ 是目标函数中基变量系数 , $a_{ij}$ 是系数矩阵中对应的 $x_j$ 非基变量列向量 ;

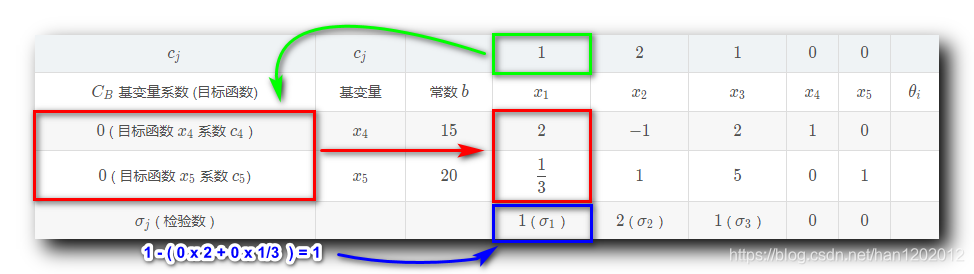
① $\sigma_1$ 检验数计算 : $\sigma_1 = 1 - ( 0 \times 2 + 0 \times \dfrac{1}{3} ) = 1$

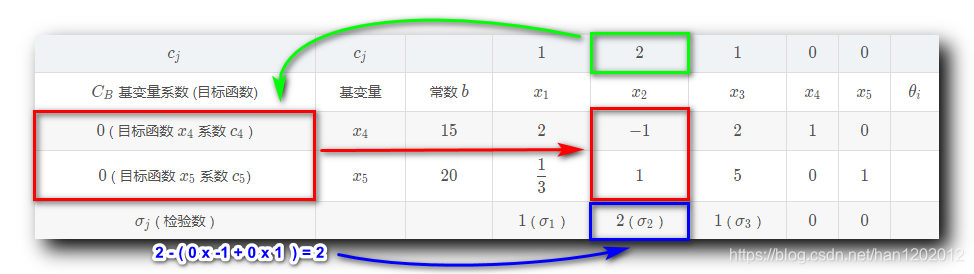
在这里插入图片描述
② $\sigma_2$ 检验数计算 : $\sigma_2 = 2 - ( 0 \times (-1) + 0 \times 1 ) = 2$

③ $\sigma_13$ 检验数计算 : $\sigma_3 = 1 - ( 0 \times 2 + 0 \times 5 ) = 1$

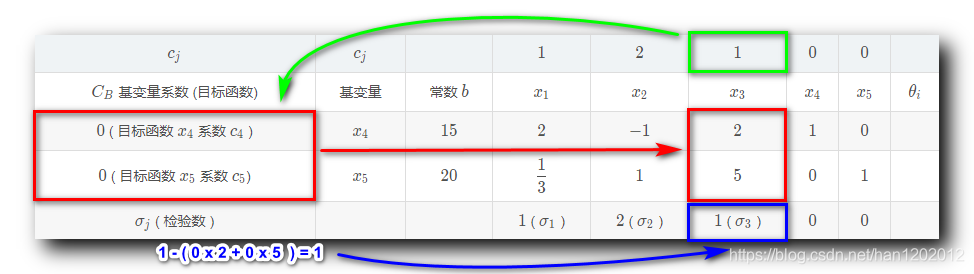
在这里插入图片描述

六、选择入基变量与出基变量

入基变量选择 : 选择检验数 $\sigma_j$ 较大的非基变量作为入基变量 , 即 $x_2$ ;

出基变量是根据 $\theta$ 值来选择的 , 选择 $\theta$ 值较小的值对应的基变量作为出基变量 ;

出基变量选择 : 常数列 $b =\begin{pmatrix} \quad 15 \quad \\ \quad 20 \quad \end{pmatrix}$ , 分别除以除以入基变量 $x_2$ 大于 $0$ 的系数列 $\begin{pmatrix} \quad -1 \quad \\\\ \quad 1 \quad \end{pmatrix}$ , 计算过程如下 $\begin{pmatrix} \quad 系数小于0 不计算 \quad \\\\ \quad \cfrac{20}{1} \quad \end{pmatrix}$ , 得出结果是 $\begin{pmatrix} \quad 无效值 \quad \\\\ \quad 20 \quad \end{pmatrix}$ , 如果系数小于等于 $0$ , 该值就是无效值 , 默认为无穷大 , 不进行比较 , 选择 $20$ 对应的基变量作为出基变量 , 查看该最小值对应的变量是 $x_5$ , 选择该 $x_5$ 变量作为出基变量 ;

在这里插入图片描述

七、第一次迭代 : 列出单纯形表

上述已经得到 $x_2$ 作为入基变量 , 由非基变量转为基变量 , $x_5$ 作为出基变量 , 由基变量转为非基变量 ; 使用 $x_2$ , 替换基变量中的 $x_5$ 的位置 ;

基变量为 $x_4 , x_2$ , 注意顺序不要写反 ;

$c_j$	$c_j$		$1$	$2$	$1$	$0$	$0$
$C_B$ 基变量系数 (目标函数)	基变量	常数 $b$	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$	$\theta_i$
$0$ ( 目标函数 $x_4$ 系数 $c_4$ )	$x_4$	$15$	$2$	$-1$	$2$	$1$	$0$	$-$ ( $\theta_4$ )
$0$ ( 目标函数 $x_5$ 系数 $c_5$ )	$x_5$	$20$	$\dfrac{1}{3}$	$1$	$5$	$0$	$1$	$20$ ( $\theta_5$ )
$\sigma_j$ ( 检验数 )			$1$ ( $\sigma_1$ )	$2$ ( $\sigma_2$ )	$1$ ( $\sigma_3$ )	$0$	$0$
第一次迭代	–	–	–	–	–	–	–	–
$0$ ( 目标函数 $x_4$ 系数 $c_4$ )	$x_4$	$15$	$?$	$1$	$?$	$1$	$?$	$?$ ( $\theta_4$ )
$2$ ( 目标函数 $x_2$ 系数 $c_2$ )	$x_2$	$20$	$?$	$0$	$?$	$0$	$?$	$?$ ( $\theta_2$ )
$\sigma_j$ ( 检验数 )			$1$ ( $\sigma_1$ )	$0$	$1$ ( $\sigma_3$ )	$0$	$?$ ( $\sigma_2$ )

【运筹学】线性规划 单纯形法 ( 案例解析 | 标准形转化 | 查找初始基可行解 | 最优解判定 | 查找入基变量与出基变量 | 第一次迭代)