Deutsch算法过程的推导
本文中的内容参考的是 Micheal A.Nielsen与Isaac L.Chuang合著的《Quantum Computation and Quantum Information》有兴趣的同学可以去阅读原文。
Deutsch算法背景介绍
假设,我们有函数f(x)f(x)f(x), 对于一个输入x∈{0,1}x\in\{0,1\}x∈{ 0,1},有f(x)f(x)f(x)或者为一个常值函数f(0)=f(1)∈{0,1}f(0)=f(1)\in\{0,1\}f(0)=f(1)∈{ 0,1}, 或者为一个平衡函数f(x)=1?xf(x)=1-xf(x)=1?x 满足 x∈{0,1}x\in\{0,1\}x∈{ 0,1}。现在的问题是我们应该如何判断f(x)f(x)f(x)是属于哪一个类别。对于经典计算机来说,我们需要两次计算即,计算f(0)f(0)f(0)与f(1)f(1)f(1), 再比较。而对于量子计算机我们只需要一次计算即可进行判断。
Deutsch算法电路图1
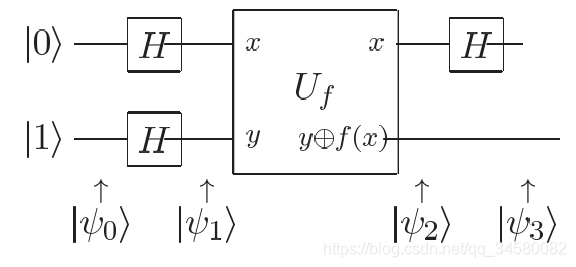
上图中的 UfU_fUf?模块的作用效果可以写成Uf:∣x?∣y?→∣x?∣y?f(x)?U_f:|x\rangle|y\rangle\rightarrow|x\rangle|y\oplus f(x)\rangleUf?:∣x?∣y?→∣x?∣y?f(x)?,容易说明UfU_fUf?是酉的。
Deutsch算法推导过程
初始状态我们可以简单写出 ∣ψ0?=∣0?∣1?|\psi_0\rangle=|0\rangle|1\rangle∣ψ0??=∣0?∣1?,在这里我们省略的张量积符号。
第一步,我们在上下两个比特上分别作用两个Hadamard门,于是我们可以得到
∣ψ1?=[∣0?+∣1?2][∣0??∣1?2]|\psi_1\rangle=[\frac{|0\rangle+|1\rangle}{\sqrt{2}}][\frac{|0\rangle-|1\rangle}{\sqrt{2}}]∣ψ1??=[2?∣0?+∣1??][2?∣0??∣1??]
第二步,我们作用构造的UfU_fUf?门可以得到
∣ψ2?=Uf∣ψ1?=12[∣0,f(0)??∣0,1?f(0)?+∣1,f(1)??∣1,1?f(1)?]|\psi_2\rangle=U_f|\psi_1\rangle=\frac{1}{2}[|0,f(0)\rangle-|0,1\oplus f(0)\rangle+|1,f(1)\rangle-|1,1\oplus f(1)\rangle]∣ψ2??=Uf?∣ψ1??=21?[∣0,f(0)??∣0,1?f(0)?+∣1,f(1)??∣1,1?f(1)?]
=12[∣0?(∣f(0)??∣1?f(0)?)+∣1?(∣f(1)??∣1?f(1)?)]=\frac{1}{2}[|0\rangle(|f(0)\rangle-|1\oplus f(0)\rangle)+|1\rangle(|f(1)\rangle-|1\oplus f(1)\rangle)]=21?[∣0?(∣f(0)??∣1?f(0)?)+∣1?(∣f(1)??∣1?f(1)?)]
此时,我们根据背景里面提到的两种情况进行讨论。
第一种情况,f(0)=f(1)f(0)=f(1)f(0)=f(1):
此时,∣ψ2?|\psi_2\rangle∣ψ2??可以重新写成
∣ψ2?=12[∣0?(∣f(0)??∣1?f(0)?)+∣1?(∣f(0)??∣1?f(0)?)]=12[∣0?+∣1?][∣f(0)??∣1?f(0)?]|\psi_2\rangle=\frac{1}{2}[|0\rangle(|f(0)\rangle-|1\oplus f(0)\rangle)+|1\rangle(|f(0)\rangle-|1\oplus f(0)\rangle)]=\frac{1}{2}[|0\rangle+|1\rangle][|f(0)\rangle-|1\oplus f(0)\rangle]∣ψ2??=21?[∣0?(∣f(0)??∣1?f(0)?)+∣1?(∣f(0)??∣1?f(0)?)]=21?[∣0?+∣1?][∣f(0)??∣1?f(0)?]
第二种情况,f(0)≠f(1)f(0)\neq f(1)f(0)?=f(1),此时,满足f(1)=1?f(0),1?f(1)=f(0)f(1)=1\oplus f(0), 1\oplus f(1)=f(0)f(1)=1?f(0),1?f(1)=f(0):
∣ψ2?=12[∣0?(∣f(0)??∣1?f(0)?)+∣1?(∣1?f(0)??∣f(0)?)]=12[∣0??∣1?][∣f(0)??∣1?f(0)?]|\psi_2\rangle=\frac{1}{2}[|0\rangle(|f(0)\rangle-|1\oplus f(0)\rangle)+|1\rangle(|1\oplus f(0)\rangle-| f(0)\rangle)]=\frac{1}{2}[|0\rangle-|1\rangle][|f(0)\rangle-|1\oplus f(0)\rangle]∣ψ2??=21?[∣0?(∣f(0)??∣1?f(0)?)+∣1?(∣1?f(0)??∣f(0)?)]=21?[∣0??∣1?][∣f(0)??∣1?f(0)?]
此时,我们对第一个qubit作用一个Hadamard门,可以看到
对于第一种情况,我们有
∣ψ3?=12∣0?[∣f(0)??∣1?f(0)?]|\psi_3\rangle=\frac{1}{\sqrt{2}}|0\rangle[|f(0)\rangle-|1\oplus f(0)\rangle]∣ψ3??=2?1?∣0?[∣f(0)??∣1?f(0)?]
对于第二种情况我们有
∣ψ3?=12∣1?[∣f(0)??∣1?f(0)?]|\psi_3\rangle=\frac{1}{\sqrt{2}}|1\rangle[|f(0)\rangle-|1\oplus f(0)\rangle]∣ψ3??=2?1?∣1?[∣f(0)??∣1?f(0)?]
所以,当我们对第一个qubit进行测量。通过测量结果,我们就可以知道关于f(x)f(x)f(x)的特性了。
图片来自于 Micheal A.Nielsen与Isaac L.Chuang合著的《Quantum Computation and Quantum Information》 ??