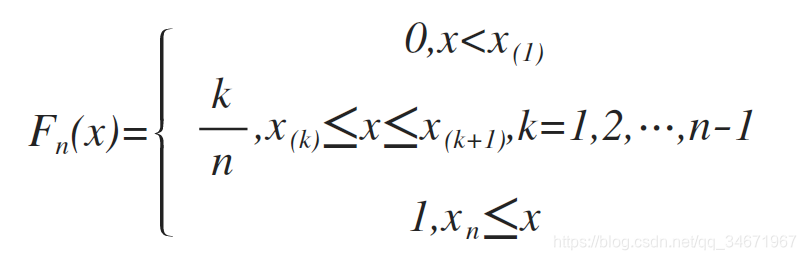数理统计内容整理（一）基本概念_综合

总体（或母体）

所研究的对象的全体。

个体

这里是引用

总体中的元素。

有限总体

总体中的个体数目为有限。

无限总体

总体中的个数数目为无线。

数理统计

关心的是某一项或若干项数量指标X（向量）和该数量指标X在总体中的分布情况。–“所谓的总体的分布就是数量指标X的分布”

样本及其分布

样本

从总体中取得一部分个体，这一部分个体成为样本（或子样）

样品

样本中的每个个体称为样本

样本容量

样本中的个体数目称为样本容量

抽样

取得样本的过程

抽样法

抽样中采用的方法

随机抽样法

从总体中随意的抽取若干个个体–一般采用此方法

样本空间

总体X随机抽样的到的样本按顺序排序用X1…Xn表示,或者用n维随即向量 $X=^(X1,? ,Xn)TX\quad \widehat { = } \quad { ({ X }_{ 1 },\cdots ,X_{ n }) }^{ T }$ 表示.
样本 $(X1,? ,Xn)T\quad { ({ X }_{ 1 },\cdots ,X_{ n }) }^{ T }$ 可能取值的全体成为样本空间

i.i.d.

独立同分布

简单随机样本

${ X }_{ 1 }$ 的分布与总体X的分布相同

分布-对于简单随机样本X1…Xn

若总体的分布函数为F(x)则样本的联合分布函数为:

$}_{ s }({ x }_{ 1 },\cdots ,{ x }_{ n }) = \prod _{ i=1 }^{ n }{ F({ x }_{ i }) }$

若总体的概率密度f(x)则样本的联合概率密度为:

$}_{ s }({ x }_{ 1 },\cdots ,{ x }_{ n }) = \prod _{ i=1 }^{ n }{ f({ x }_{ i }) }$

若总体具有分布律(概率函数)p(x),其中p(ai) = P(X = ai),则样本的联合概率函数为:

$}_{ s }({ x }_{ 1 },\cdots ,{ x }_{ n })=\prod _{ i=1 }^{ n }{ p({ x }_{ i }) }$

统计量

样本均值

$Xˉ=1n∑i=1nXi\bar { X } =\frac { 1 }{ n } \sum _{ i=1 }^{ n }{ { X }_{ i } }$

样本方差

$}^{ 2 }=\frac { 1 }{ n } \sum _{ i=1 }^{ n }{ { ({ X }_{ i }-\overline { X } ) }^{ 2 } } =\frac { 1 }{ n } \sum _{ i=1 }^{ n }{ { { X }_{ i } }^{ 2 } } -{ \overline { X } }^{ 2 }$

修正样本方差

$}^{ *2 }=\frac { 1 }{ n-1 } \sum _{ i=1 }^{ n }{ { ({ X }_{ i }-\overline { X } ) }^{ 2 } }$

样本k阶原点矩

$}_{ k }=\frac { 1 }{ n } \sum _{ i=1 }^{ n }{ { X }_{ i }^{ k } }$

样本k阶中心距

$Bk=1n∑i=1n(Xi?X?)kB_{ k }=\frac { 1 }{ n } \sum _{ i=1 }^{ n }{ { ({ X }_{ i }-\overline { X } ) }^{ k } }$

X(k)的概率密度f(k)(x)(1<=k<=n)

$}_{ (k) }(x)=\frac { n! }{ (k-1)!(n-k)! } { [F(x)] }^{ k-1 }{ [1-F(x)] }^{ n-k }f(x)$

X(k)与X(j)的联合概率密度f(k)(j)(x,y)(1<=k<=j<=n)

$}_{ (k)(j) }(x,y)=\frac { n! }{ (k-1)!(j-k-1)!(n-j)! } { [F(x)] }^{ k-1 }{ [F(y)-F(x)] }^{ j-k-1 }{ [1-F(y)] }^{ n-j }f(x)f(y)$

在顺序统计量中

样本中位数

$\{ }_{ \frac { 1 }{ 2 } ({ X }_{ n/2 }+{ X }_{ (n/2+1) }),\quad \quad \quad n为偶数 }^{ { X }_{ ((n+1)/2) },\quad \quad \quad \quad \quad n为奇数 }$
观察值为
$\{ }_{ \frac { 1 }{ 2 } ({ x }_{ n/2 }+{ x }_{ (n/2+1) }),\quad \quad \quad n为偶数 }^{ { x }_{ ((n+1)/2) },\quad \quad \quad \quad \quad n为奇数 }$

样本极差

$R={ X }_{ (n) } - { X }_{ (1) }$
其观察值为
$r={ x }_{ (n) } - { x }_{ (1) }$

经验分布函数

抽样分布

所谓抽样分布是指统计量的概率分布,确定统计量的分布是数理统计学的基本问题之一.一般情况下,统计量分布的推导问题可分为两种情况进行讨论:(1)当已知总体X的分布时,若对任意容量为n的样本 ${ X }_{1},...{X}_{n}$ 能求出统计量g( ${ X }_{1},...{X}_{n}$ )的分布,则称该分布为g( ${ X }_{1},...{X}_{n}$ )的精确分布.确定统计量的精确分布,对于数理统计中的所谓小样问题(指样本容量n较小时的统计问题)的研究是很重要的;(2)当n->∞时,能求出统计量g( ${ X }_{1},...{X}_{n}$ )的极限分布.统计量的极限分布对于数理统计中得到的所谓大样问题(指样本容量n较大时的统计问题)的研究是非常有用的.

Γ分布

若随机变量X具有概率密度
$f(x,α,λ)={0,x≤0λαΓ(α)xα?1e?λx,x>0f(x,\alpha ,\lambda )={ \{ }_{ 0,x\le 0 }^{ \frac { { \lambda }^{ \alpha } }{ \Gamma (\alpha ) } { x }^{ \alpha -1 }{ e }^{ -\lambda x },x>0 }$
则成X服从参数为α、λ的Γ分布,记为 $}\sim \Gamma (\alpha ,\lambda )$ ,其中α>0,λ>0为参数.

Γ函数

$Γ(α)=∫0+∞xα?1e?xdx\Gamma (\alpha )=\int _{ 0 }^{ +\infty }{ { x }^{ \alpha -1 }{ e }^{ -x }dx }$

Γ引申

$(\alpha +1)=\alpha \Gamma (\alpha )(因而\Gamma (n+1)=n!)$
$Γ(1)=1\Gamma (1)=1$
$Γ(12)=π\Gamma (\frac { 1 }{ 2 } )=\sqrt { \pi }$
$Γ(p)Γ(q)Γ(p+q)=B(p,q)\frac { \Gamma (p)\Gamma (q) }{ \Gamma (p+q) } =B(p,q)$

性质1

若 $X?Γ(α,λ)X\sim \Gamma (\alpha ,\lambda )$ ,则 $E(X)=αλ,D(X)=αλ2.E(X)=\frac { \alpha }{ \lambda } ,D(X)=\frac { \alpha }{ { \lambda }^{ 2 } } .$

性质2(可加性)

$}_{ i }\sim \Gamma ({ \alpha }_{ i },\lambda ),i=1,\cdots ,n,且{ X }_{ 1 },\cdots ,{ X }_{ n }相互独立,则:$
$}_{ 1 }+\cdots +{ X }_{ n }\sim \Gamma ({ \alpha }_{ 1 }+\cdots +{ \alpha }_{ n },\lambda ).$

β分布

若随机变量X具有概率密度
$f(x;α,b)={0,其他xa?1(1?x)b?1B(a,b),0<x<1f(x;\alpha ,b)={ \{ }_{ 0,其他 }^{ \frac { { x }^{ a-1 }{ (1-x) }^{ b-1 } }{ B(a,b) } ,0<x<1 }$
则称X服从参数为a、b的β分布,记为 $}\sim β (a ,b)$ ,其中a>0,b>0为参数.

β函数

$B(p,q)=∫01xp?1(1?x)q?1dxB(p,q)=\int _{ 0 }^{ 1 }{ { x }^{ p-1 }{ (1-x) }^{ q-1 }dx }$

性质1

若 $X?β(a,b)X\sim \beta (a,b)$ ,则
$E(X)=aa+b,D(X)=ab(a+b)2(a+b+1)E(X)=\frac { a }{ a+b } ,D(X)=\frac { ab }{ { (a+b) }^{ 2 }(a+b+1) }$

性质2

若 $X?Γ(a,1),Y?Γ(b,1)X\sim \Gamma (a,1),Y\sim \Gamma (b,1)$ 且X,Y相互独立,则
$Z=XX+Y?β(a,b)Z=\frac { X }{ X+Y } \sim \beta (a,b)$

$\chi }^{ 2 }分布$

若随机变量X具有概率密度
$\chi }^{ 2 }(x;n)={ \{ }_{ 0,x\le 0 }^{ \frac { { x }^{ \frac { n }{ 2 } -1 }{ e }^{ -\frac { x }{ 2 } } }{ { 2 }^{ \frac { n }{ 2 } }\Gamma (\frac { n }{ 2 } ) } ,x>0 }$
则称X服从自由度为n的 $\chi }^{ 2 }分布$ ,记为 $X?χ2(n).X\sim { \chi }^{ 2 }(n).$ 随机变量X称为 $\chi }^{ 2 }$ 变量.

性质1

若 $X?χ2(n)X\sim { \chi }^{ 2 }(n)$ ,则 $E (X) = n, D (X) = 2 n$ .

性质2(可加性)

$}_{ i }\sim { \chi }^{ 2 }({ n }_{ i }),i=1,\cdots ,k且{ X }_{ i },\cdots ,{ X }_{ k }相互独立,则$
$}_{ 1 }+\cdots +{ X }_{ k }\sim { \chi }^{ 2 }({ n }_{ 1 }+\cdots +{ n }_{ k }).$

定理

设随机变量 $}_{ 1 },\cdots ,{ X }_{ n }$ 相互独立,且都服从标准正态分布N(0,1),则随机变量
$\chi }^{ 2 }=\sum _{ i=1 }^{ n }{ { X }_{ i }^{ 2 } }$ 服从自由度为n的 $\chi }^{ 2 }分布$ ,即 $\chi }^{ 2 }\sim { \chi }^{ 2 }(n)$

t分布

若随机变量T具有概率密度
$t(x;n)=Γ(n+12)nπΓ(n2)(1+x2n)?n+12,?∞<x<+∞t(x;n)=\frac { \Gamma (\frac { n+1 }{ 2 } ) }{ \sqrt { n\pi } \Gamma (\frac { n }{ 2 } ) } { (1+\frac { { x }^{ 2 } }{ n } ) }^{ -\frac { n+1 }{ 2 } },-\infty <x<+\infty$
则称T服从自由度为n的t分布,记为T~t(n).t分布又称为学生分布.

定理

$若X?N(0,1),Y?χ2(n),且X与Y相互独立,则若X\sim N(0,1),Y\sim { \chi }^{ 2 }(n),且X与Y相互独立,则$
$T=XYn?t(n)T=\frac { X }{ \sqrt { \frac { Y }{ n } } } \sim t(n)$

F分布

若随机变量F具有概率密度
$}_{ 1 },{ n }_{ 2 })={ \{ }_{ 0,x\le 0 }^{ \frac { \Gamma (\frac { { n }_{ 1 }+{ n }_{ 2 } }{ 2 } ) }{ \Gamma (\frac { { n }_{ 1 } }{ 2 } )\Gamma (\frac { { n }_{ 2 } }{ 2 } ) } (\frac { { n }_{ 1 } }{ { n }_{ 2 } } ){ (\frac { { n }_{ 1 } }{ { n }_{ 2 } } x) }^{ \frac { { n }_{ 1 } }{ 2 } -1 }{ (1+\frac { { n }_{ 1 } }{ { n }_{ 2 } } x) }^{ -\frac { { n }_{ 1 }+{ n }_{ 2 } }{ 2 } },x>0 }$
则称F服从自由度为 ${ n }_{ 1 },{ n }_{ 2 })$ 的F分布,记为 $F?F(n1,n2).F\sim F({ n }_{ 1 },{ n }_{ 2 }).$

定理

$若X?χ2(n1),Y?χ2(n2),且X与Y相互独立,则若X\sim { \chi }^{ 2 }({ n }_{ 1 }),Y\sim { \chi }^{ 2 }({ n }_{ 2 }),且X与Y相互独立,则$
$F=Xn1Yn2?F(n1,n2)F=\frac { \frac { X }{ { n }_{ 1 } } }{ \frac { Y }{ { n }_{ 2 } } } \sim F({ n }_{ 1 },{ n }_{ 2 })$

推论

$在定理的条件下,若F?F(n1,n2),则1F?F(n2,n1).在定理的条件下,若F\sim F({ n }_{ 1 },{ n }_{ 2 }),则\frac { 1 }{ F } \sim F({ n }_{ 2 },{ n }_{ 1 }).$

分位数

$设随机变量X的分布函数为F(x)=P{X≤x},对于0<p<1,若有xp满足设随机变量X的分布函数为F(x)=P\{ X\le x\} ,对于0<p<1,若有{ x }_{ p }满足$
$P{X≤xp}=F(xp)=pP\{ X\le { x }_{ p }\} =F({ x }_{ p })=p$
$}_{ p }为分布F(x)(或随机变量X)的下侧p分位数;对于0<\alpha <1,若有{ y }_{ \alpha }满足$
$P{X>yα}=1?F(yα)=αP\{ X>{ y }_{ \alpha }\} =1-F({ y }_{ \alpha })=\alpha$
$}_{ \alpha }为分布F(x)(或随机变量X)的上侧\alpha 分位数.$
$}_{ \alpha }={ x }_{ 1-\alpha };{ x }_{ p }={ y }_{ 1-p }$

正态总体的抽样分布

定理1

$}_{ 1 },\cdots ,{ X }_{ n }是来自正态总体N(\mu ,{ \sigma }^{ 2 })的样本,\overline { X } 为样本均值,{ S }^{ *2 }为修正样本方差,则$
(1) $X??N(μ,σ2n);\overline { X } \sim N(\mu ,\frac { { \sigma }^{ 2 } }{ n } );$
(2) $(n?1)S?2σ2=nS2σ2=1σ2∑i=1n(Xi?X?)2?χ2(n?1);\frac { (n-1){ S }^{ *2 } }{ { \sigma }^{ 2 } } =\frac { n{ S }^{ 2 } }{ { \sigma }^{ 2 } } =\frac { 1 }{ { \sigma }^{ 2 } } \sum _{ i=1 }^{ n }{ { ({ X }_{ i }-\overline { X } ) }^{ 2 } } \sim { \chi }^{ 2 }(n-1);$
(3) $X?与S?2相互独立\overline { X } 与{ S }^{ *2 }相互独立$

定理2

$}_{ 1 },\cdots ,{ X }_{ { n } }为正态总体N(\mu ,{ \sigma }^{ 2 })的样本,\overline { X } 为样本均值,{ S }^{ *2 }为修正样本方差,则$
$T=n(X??μ)S??t(n?1)T=\frac { \sqrt { n } (\overline { X } -\mu ) }{ { S }^{ * } } \sim t(n-1)$

定理3

$}_{ 1 },\cdots ,{ X }_{ { n }_{ 1 } }和{ Y }_{ 1 },\cdots ,{ Y }_{ { n }_{ 2 } }分别为正态总体N({ \mu }_{ 1 },{ \sigma }^{ 2 })和N({ \mu }_{ 2 },{ \sigma }^{ 2 })的样本,且两样本相互独立,记$
$X?=1n1∑i=1n1Xi,Y?=1n2∑i=1n2Yi,S1n1?2=1n1?1∑i=1n1(Xi?X?)2,S2n2?2=1n2?1∑i=1n2(Yi?Y?)2,则有\overline { X } =\frac { 1 }{ { n }_{ 1 } } \sum _{ i=1 }^{ { n }_{ 1 } }{ { X }_{ i } } ,\\ \overline { Y } =\frac { 1 }{ { n }_{ 2 } } \sum _{ i=1 }^{ { n }_{ 2 } }{ { Y }_{ i } } ,\\ { S }_{ { 1 }_{ { n }_{ 1 } } }^{ *2 }=\frac { 1 }{ { n }_{ 1 }-1 } \sum _{ i=1 }^{ { n }_{ 1 } }{ { ({ X }_{ i }-\overline { X } ) }^{ 2 } } ,\\ { S }_{ { 2 }_{ { n }_{ 2 } } }^{ *2 }=\frac { 1 }{ { n }_{ 2 }-1 } \sum _{ i=1 }^{ { n }_{ 2 } }{ { ({ Y }_{ i }-\overline { Y } ) }^{ 2 } } ,则有$
$T=(X??Y?)?(μ1?μ2)Sω1n1+1n2?t(n1+n2?2)T=\frac { (\overline { X } -\overline { Y } )-({ \mu }_{ 1 }-{ \mu }_{ 2 }) }{ { S }_{ \omega }\sqrt { \frac { 1 }{ { n }_{ 1 } } +\frac { 1 }{ { n }_{ 2 } } } } \sim t({ n }_{ 1 }+{ n }_{ 2 }-2)$
其中
$}_{ \omega }=\sqrt { \frac { ({ n }_{ 1 }-1){ S }_{ { 1 }_{ { n }_{ 1 } } }^{ *2 }+({ n }_{ 2 }-1){ S }_{ { 2 }_{ { n }_{ 2 } } }^{ *2 } }{ { n }_{ 1 }+{ n }_{ 2 }-2 } }$

定理4

$}_{ 1 },\cdots ,{ X }_{ { n }_{ 1 } }和{ Y }_{ 1 },\cdots ,{ Y }_{ { n }_{ 2 } }分别为正态总体N({ \mu }_{ 1 },{ { \sigma }_{ 1 } }^{ 2 })和N({ \mu }_{ 2 },{ { \sigma }_{ 2 } }^{ 2 })的样本,且两样本相互独立,{ S }_{ { 1 }_{ { n }_{ 1 } } }^{ *2 }和{ S }_{ { 2 }_{ { n }_{ 2 } } }^{ *2 }分别为两个样本各自的修正方差,则$
$F=σ22S1n1?2σ12S2n2?2?F(n1?1,n2?1)F=\frac { { \sigma }_{ 2 }^{ 2 }{ S }_{ { 1 }_{ { n }_{ 1 } } }^{ *2 } }{ { \sigma }_{ 1 }^{ 2 }{ S }_{ { 2 }_{ { n }_{ 2 } } }^{ *2 } } \sim F({ n }_{ 1 }-1,{ n }_{ 2 }-1)$

定理5(柯赫伦)-该定理在方差分析和回归分析中具有重要作用.

$}_{ 1 },\cdots ,{ X }_{ n }是n个相互独立的标准正态变量,记Q=\sum _{ i=1 }^{ n }{ { X }_{ i }^{ 2 } } .若Q可以分解为\\ Q={ Q }_{ 1 }+\cdots +{ Q }_{ k }\\ 其中{ Q }_{ i }(i=1,\cdots ,k)是{ X }_{ 1 },\cdots ,{ X }_{ n }的秩为{ n }_{ i }的非负定二次型,$
$}_{ 1 },\cdots ,{ Q }_{ k }相互独立,且{ Q }_{ i }\sim { \chi }^{ 2 }({ n }_{ i })(i=1,\cdots ,k)的充分必要条件是\\ \sum _{ i=1 }^{ k }{ { n }_{ i } } =n$

正态标准化

$X?N(μ,σ2)X\sim N(\mu ,{ \sigma }^{ 2 })$
$X?μσ?N(0,1)\frac { X-\mu }{ \sigma } \sim N(0,1)$
$Xˉ?N(μ,σ2n)\bar { X } \sim N(\mu ,\frac { { \sigma }^{ 2 } }{ n } )$
$n(Xˉ?μ)σ?N(0,1)\frac { \sqrt { n } (\bar { X } -\mu ) }{ \sigma } \sim N(0,1)$

置信区间( $X?\overline {X}$ -△, $X?\overline {X}$ +△)

当 $σ\sigma$ 已知

△= $\mu }_{ \frac { \alpha }{ 2 } }\frac { \sigma }{ \sqrt { n } }$

当 $σ\sigma$ 未知

△= $}_{ \frac { \alpha }{ 2 } }(n-1)\frac { S }{ \sqrt { n } }$

各种分布的方程

二项分布X~B(n,p),则随机变量X的分布列为

P(X=k)= ${C}_{n}^{k}$ p^k (1-p)^n-k k=0,1,…,n
$μ=np\mu=np$
$σ2=npq{\sigma}^{2}=npq$

泊松分布X~P(λ)

P(X=k)= $λke?λk!\frac { { \lambda }^{ k }{ e }^{ -\lambda } }{ k! }$ ,λ>0,k=0,1…
$μ=λ\mu=\lambda$
$σ2=λ{\sigma}^{2}=\lambda$

均匀分布X~U(a,b)

$f(x)={1b?a0,其他,a≤x≤bf\left( x \right) =\begin{cases} \frac { 1 }{ b-a } \\ 0,其他 \end{cases},a\le x\le b$
$μ=a+b2\mu=\frac { a+b }{ 2 }$
$σ2=(b?a)212{\sigma}^{2}=\frac { {(b-a)}^{2} }{ 12 }$

指数分布X~Exp(λ)

$f(x)={λe?λx,x>00,x≤0f\left( x \right) =\begin{cases} \lambda { e }^{ -\lambda x },x>0 \\ 0,x\le 0 \end{cases}$
$μ=1λ\mu=\frac { 1 }{ \lambda }$
$σ2=1λ2{\sigma}^{2}=\frac { 1 }{ {\lambda}^{2} }$

正态分布X~( $μ,σ2\mu,{\sigma}^{2}$ )

$f(x)=1σ2πe?(x?μ)22σ2f\left( x \right) =\frac { 1 }{ \sigma \sqrt { 2\pi } } { e }^{ -\frac { { (x-\mu ) }^{ 2 } }{ 2{ \sigma }^{ 2 } } }$

用概率密度求均值

$μ=概率密度的积分\mu=概率密度的积分$

用极差R求标准差的估计

$σ^=Rdn\hat \sigma=\frac {R}{ {d}_{n}}$ n为样本个数 ${d}_{n}$ 可查表得

数理统计内容整理（一）基本概念