Logistic Regression 笔记与理解
Logistic Regression
Hypothesis 记为 H(theta)
H(theta)=g(z)
其中g(z),是一个叫做Logistic Function的函数,g(z)函数定义如下:
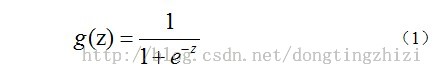
对应图像如下:
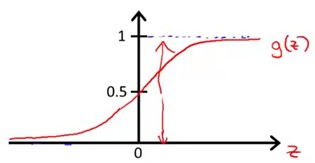
这是一个值域为0~1的s型函数,在理解中可以认为:
落在曲线上的任意一点A
A的横坐标对应的纵坐标值是z参数,或者说z对象属于“1”的概率。
在Logistic Regression中
g(z)的参数z为:
一个线性或非线性函数的向量化表示
这个函数对应的图像被称作决策边界
两种决策边界的例子:
线性:
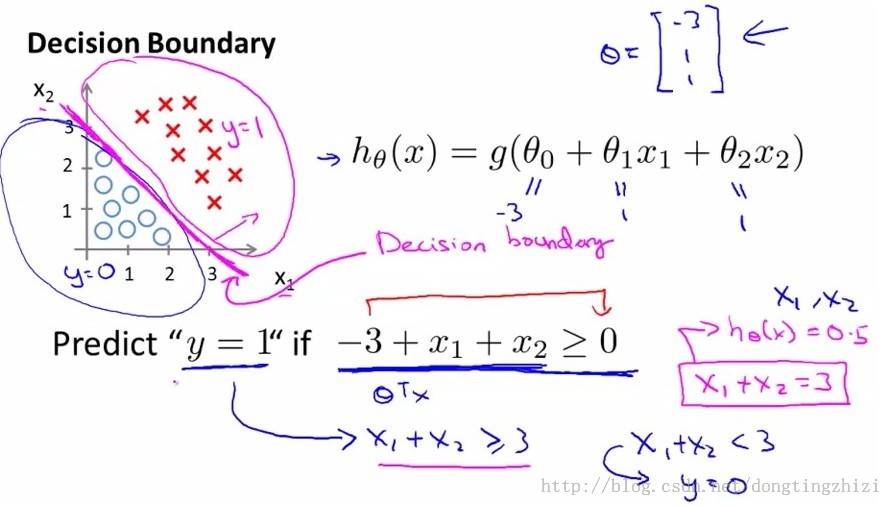
非线性:

为了方便,以下我们只讨论线性边界的情况
线性边界的表示为
X’*theta
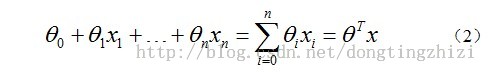
所以Logistic Regression Hypothesis 定义如下:
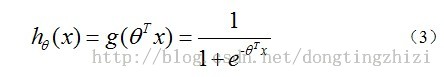
如上所说,Hypothesis定义了结果取1的概率,因此对于输入x分类结果为类别1和类别0的概率分别为:
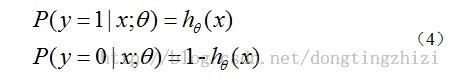
以上是Logistic Regression Hypothesis 的理解
Logistic Regression Cost Function 记为 J(theta)
Cost 的主要功能是计算H(theta)和答案Y的差距,在线性回归中这个差距可以用方差解决,但是Logistic问题只有+-两种答案,所以Logistic Regression的Cost函数应该是这样的:
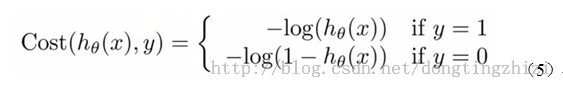
整合为一个函数
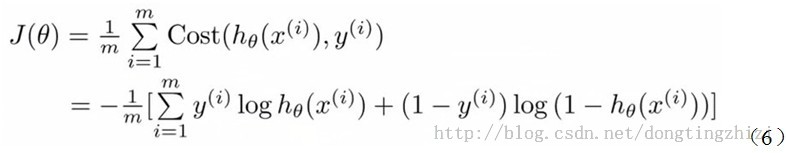
我们便得到了Logistic Regression的Cost Function。
接下来就是求解Cost Function最小值的方法-梯度下降
或使用Matlab 内建miniziae函数