主成份分析: Principle Component Analysis (PCA)
主成份分析是一种特征降维方法,降维后的结果要保持原始数据固有结构。
原始数据结构:
- 图像数据中结构:视觉对象区域构成的空间分布
- 文本数据中结构:单词之间的(共现)相似或不相似

主成份分析中若干概念-方差与协方差
1、数据样本的方差(variance)描述了样本数据的波动程度
假设有?个数据,记为? = {?? } (? = ?, … , ?)

2、数据样本的协方差 (covariance) 衡量两个变量之间的相关度
假设有?个两维变量数据,记为(?, ?) = {(?? , ??)} (? = ?, … , ?)


对于一组两维变量(如广告投入-商品销售、天气状况-旅游出行等),可通过计算它们之间的协方差值来判断这组数据给出的两维变量是否存在关联关系:
- 当协方差??? ?, ? > 0 时,称? 与? 正相关
- 当协方差??? ?, ? < 0 时,称? 与? 负相关
- 当协方差??? ?, ? = 0 时,称? 与? 不相关(线性意义下)
方差与协方差的关系
方差是用来度量单个变量 “ 自身变异”大小的总体参数,方差越大表明该变量的变异越大
协方差是用来度量两个变量之间 “协同变异”大小的总体参数,即二个变量相互影响大小的参数,协方差的绝对值越大,则二个变量相互影响越大。
协方差矩阵:
- 协方差矩阵能处理多维问题;
- 协方差矩阵是一个对称的矩阵,而且对角线是各个维度上的方差。
- 协方差矩阵计算的是不同维度之间的协方差,而不是不同样本之间的。
- 样本矩阵中若每行是一个样本,则每列为一个维度,所以计算协方差时要按列计算均值。
我们可通过皮尔逊相关系数(Pearson Correlation coefficient )将两组变量之间的关联度规整到一定的取值范围内。皮尔逊相关系数定义如下:
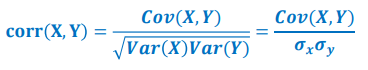

皮尔逊相关系数所具有的性质如下:
- |???? (?, ?) | ≤ 1
- ???? (?, ?) = 1的充要条件是存在常数?和?,使得? = ?? + ?
- 皮尔逊相关系数是对称的,即???? (?, ?) = ????(?, ?)
- 由此衍生出如下性质:皮尔逊相关系数刻画了变量?和?之间线性相关程度,如果|???? (?, ?) | 的取值越大,则两者在线性相关的意义下相关程度越大。 ???? (?, ?) = 0表示两者不存在线性相关关系(可能存在其他非线性相关的关系)。
- 正线性相关意味着变量?增加的情况下,变量?也随之增加;负线性相关意味着变量?减少的情况下,变量?随之增加。
相关性(correlation)与独立性(independence)
- 如果?和?的线性不相关,则 ????( ?, ?) = 0
- 如果?和?的彼此独立,则一定 ???? (?, ?) = 0,且?和?不存在任何线性或非线性关系
- “不相关”是一个比“独立”要弱的概念,即独立一定不相关,但是不相关不一定相互 独立(可能存在其他复杂的关联关系)。独立指两个变量彼此之间不相互影响。
主成份分析的算法动机是 保证样本投影后方差最大
在降维之中,需要尽可能将数据向方差最大方向进行投影,使得数据所蕴含信息没有丢失,彰显个性。如左下图所示,向?方向投影(使得二维数据映射为一维)就比向?方向投影结果在 降维这个意义上而言要好;右下图则是黄线方向投影要好。

主成份分析思想是将?维特征数据映射到 ? 维空间( ? ? ?),去除原始数据之间的冗余性(通过去除相关性手段达到这一目的)。
- 将原始数据向这些数据方差最大的方向进行投影。一旦发现了方差最大的投影方向, 则继续寻找保持方差第二的方向且进行投影。
- 将每个数据从?维高维空间映射到 ? 维低维空间,每个数据所得到最好的 ? 维特征就是使得每一维上样本方差都尽可能大。
算法描述
? 假设有 ? 个 ? 维样本数据所构成的集合 :
![]()
? 集合 ? 可以表示成一个 ? × ? 的矩阵 ? 。
? 假定每一维度的特征均值均为零(已经标准化)。
? 主成分分析的目的是求取一个且使用一个 ? × ? 的映射矩阵 ? 。
? 给定一个样本 ??,可将 ?? 从 ? 维空间如下映射到 ? 维空间 : ![]()
? 将所有降维后数据用 ? 表示 :


关于上面涉及的线代知识可参考:如何理解特征值和特征向量,
协方差矩阵怎么求
协方差矩阵计算方法

可见,在主成份分析中,最优化的方差等于原始样本数据?的协方差矩阵 ? 的特征根之和。 要使方差最大,我们可以求得协方差矩阵?的特征向量和特征根,然后取前 ? 个最大特征根所对应的特征向量组成映射矩阵 ? 即可。 注意,每个特征向量??与原始数据??的维数是一样的,均为?。
主成份分析总结:
